树和二叉树
树(Tree)
定义
n个结点的有限集(空或非空)
对于非空树
- 有且仅有一个称之为根的结点
- 除根结点外其余结点可分为m个互不相交的有限集,每个集合本身又是一棵树,称为根的子树(SubTree)
基本术语
| 术语 | 定义 |
|---|---|
| 结点 | 树的数据元素 |
| 结点的度 | 结点挂接的子树数 |
| 结点的层次 | 从根到该结点的层数(根结点算第一层) |
| 终端结点 | 度为0的结点(叶子) |
| 分支结点 | 度不为0的结点 |
| 树的度 | 所有结点度中的最大值 |
| 树的深度 | 所有结点中最大的层数 |
| 根 | 根结点(没有前驱) |
| 叶子 | 终端结点(没有后继) |
| 森林 | 指m棵不相交的树的集合 |
| 有序树 | 结点各子树从左至右有序,不能互换 |
| 无序树 | 结点各子树可互换位置 |
| 双亲和孩子 | 结点的子树的根称为该结点的孩子,该结点称为孩子的双亲 |
| 兄弟 | 同一双亲下的同层结点(孩子间 互称兄弟) |
| 堂兄弟 | 双亲位于同一层的结点(但非同一双亲) |
| 祖先 | 从根到节结点所经分支的所有结点 |
| 子孙 | 该结点下层子树中的任一结点 |
二叉树
基本定义与树差不多
不同点
- 二叉树每个结点至多只有两棵子树(即二叉树中不存在度大于2的结点)
- 二叉树有左右之分,其次序不能颠倒
选择二叉树而不是普通树运算原因:
- 二叉树结构最简单,规律性最强
- 所有树都能转为唯一对应的二叉树,不失一般性
性质
- 在第i层上之多有2$^{i-1}$个结点,至少1个
- 深度为k的二叉树至多有2$^{k}$-1个结点,至少k个
- 若2度的结点有n$_{2}$个,则叶子数n$_{0}$=n$_{2}$+1
特殊形态二叉树
满二叉树:深度为k且有2$^{k}$-1个结点的二叉树(每层都充满了结点)
完全二叉树:深度为k,有n个结点的二叉树,当且仅当每一个结点都与深度为k的满二叉树中编号从1-n的结点一一对应(最后一层叶子不满,且集中在左边)
满是完全二叉树的一个特例
一棵完全二叉树有n个结点,则叶结点的数为[(n+1)/2](向下取整),当n为奇数时,由完全二叉树的性质,n$_{1}$(度为1的结点)为1,n$_{0}$=(n+1)/2;n为偶数时,n$_{1}$为0,n$_{0}$=n/2
- 具有n个结点的完全二叉树的深度必为[log$_{2}$n]+1
- 对完全二叉树,若从上至下、从左至右编号,则编号为i的结点,其左孩子编号必为2i,有孩子编号必为2i+1,双亲编号必为i/2
顺序存储
按照满二叉树的结点层次编号,依次存放二叉树中的数据元素
链式存储
用链表来表示二叉树,通常时链表每个结点由三个域组成,数据与和左右指针域,指针域分别存储该结点左右孩子所在链结点的存储地址
二叉链
存放了左孩子和右孩子的指针
n个结点的二叉链中有n+1个空指针域(除根结点外每个结点都有且仅有1个双亲,所以有n-1个结点的链域存放指针)
三叉链
多存放了个双亲指针
遍历二叉树(递归法)
按某条搜索路线遍访每个结点且不重复(插入、删除、修改、查找、排序等)
遍历规则:先左后右
- DLR:先序遍历,先根再左后右
- LDR:中序遍历,先左再根后右
- LRD:后序遍历,先左再右后根
三种方法访问路径相同,只是访问结点的时机不同
由二叉树的前序序列和中序序列、或者后序序列和中序序列均能唯一地确定一棵二叉树,但前序序列和后序序列却无法唯一确定
二叉树建立
void CreateBiTree(BiTree &T){
cin>>ch;
if (ch==’#’)
T=NULL; //递归结束,建空树
else{
T=new BiTNode;
T->data=ch; //生成根结点
CreateBiTree(T->lchild); //递归创建左子树
CreateBiTree(T->rchild); //递归创建右子树
}
} 求二叉树结点总数
int NodeCount(BiTree T){
if(T == NULL )
return 0;
else
return NodeCount(T->lchild)+NodeCount(T->rchild)+1;
} 求二叉树叶子结点总数
int LeafCount(BiTree T){
if(T==NULL) //如果是空树返回0
return 0;
if (T->lchild == NULL && T->rchild == NULL)
return 1; //如果是叶子结点返回1
else
return LeafCount(T->lchild) + LeafCount(T->rchild);
}求二叉树深度
int Depth(BiTree T)
{
if(T==NULL)
return 0;
else
{
m = Depth(T->lchild);
n = Depth(T->rchild);
if(m > n)
return (m+1);
else
return (n+1);
}
}线索化二叉树
利用二叉链表空闲区存放当前结点的直接前驱和后继等线索,加快查找速度
- 若结点有左子树,则lchild指向其左孩子,否则指向其直接前驱(即线索)
- 若结点有右子树,则rchild指向其右孩子,否则指向其直接后继(即线索)
- 增加两个标志域LTag和RTag
若LTag=0,lchild指向其左孩子
若LTag=1,lchild指向其前驱
若RTag=0,lchild指向其右孩子
若RTag=1,lchild指向其后继
树和森林
树的存储结构
- 双亲表示法
- 孩子表示法
孩子兄弟法
typedef struct CSNode{ ElemType data; struct CSNode *firstchild, *nextsibling; } CSNode,*CSTree;
森林和二叉树转换
森林:F={T$_{1}$, T$_{2}$, ……T$_{m}$} 二叉树B=(root, LB, RB)
森林=》二叉树
- 若F为空,即m=0,则B为空树
- 若F非空,则B的根root即为森林中的第一棵树的根ROOT(T~1~),B的左子树LB是从T~1~中根结点的子树森林F$_{1}$={T$_{11}$, T$_{12}$, ……T$_{1m}$}转换而成的二叉树,右子树RB是从森林F'={T$_{2}$, T$_{3}$, ……T$_{m}$}转换而成的二叉树
二叉树=》森林
哈夫曼树及其应用
哈夫曼树
- 路径:由一结点到另一结点间的分支所构成
- 路径长度:路径上的分支数目
- 带权路径长度:结点到根的路径长度于结点上权的乘积
- 树的带权路径长度:树中所有叶子结点的带权路径长度之和
$$ WPL=\sum_{k=1}^nw_kl_k $$
- 哈夫曼树:带权路径长度最小的树
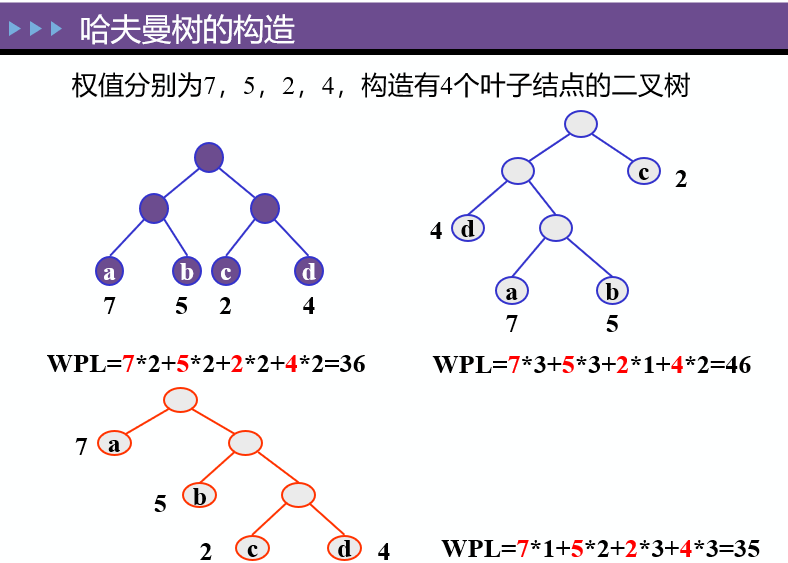
哈夫曼树构造:使权大的结点靠近根
操作:对权值的合并、删除、替换总是合并当前值最小的两个
应用
哈夫曼编码的构造:概率大的字符用短码,小的用长码,构造哈夫曼树
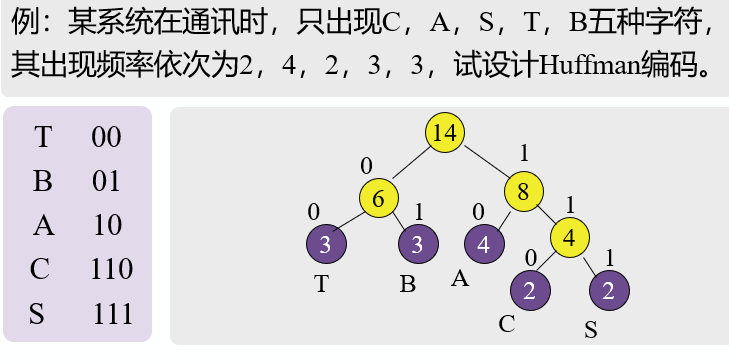
typedef struct
{
int weght;
int parent,lch,rch;
}*HuffmanTree;void CreatHuffmanTree (HuffmanTree HT,int n){
if(n<=1)
return;
m=2*n-1;
HT=new HTNode[m+1];//0号单元未用,HT[m]表示根结点
for(i=1;i<=m;++i)
{
HT[i].lch=0;
HT[i].rch=0;
HT[i].parent=0;
}
for(i=1;i<=n;++i)
cin>>HT[i].weight;
}