Loading... # 查找 ## 查找的基本概念 查找表:由同一类型的数据元素(或记录)构成的集合 关键字:数据元素(或记录)中某个数据项的值,用它可以标识一个数据元素(或记录) * 主关键字:可以唯一地标识一个记录的关键字 * 次关键字:用以识别若干记录的关键字 查找:根据给定的值,在查找表中确定一个其关键字等于给定值的记录或数据元素 动态查找表/静态查找表:查找的同时对表进行修改操作(插入/删除),即创建表,则该表称为动态查找表,否则为静态查找表 平均查找长度:为确定记录在查找表中的位置,需和给定值进行比较的关键字个数的期望值(ASL) 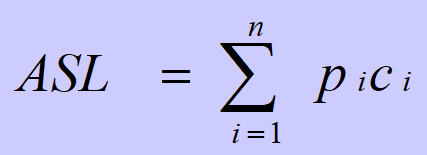 * n:记录的个数 * p$_{i}$:查找第i个记录的概率 * c$_{i}$:找到第i个记录所需的比较次数 ## 线性表的查找 ### 顺序查找 从表的一端开始,依次将记录的关键字和给定值进行比较,若某个记录的关键字和给定值相等,则查找成功;反之,若扫描整个表后,仍未找到关键字和给定值相等的数据,则查找失败 适用于线性表的顺序存储结构、链式存储结构 ~~~C typedef struct { ElemType *R; //表基址 int length; //表长 }SSTable; ~~~ #### 普通顺序查找 ~~~C int Search_Seq(SSTable ST, KeyType key) { for(int i = ST.length; i>=1; --i) if(ST.R[i].key == key) return i; return 0; } ~~~ #### 改进-->设置监视哨的顺序查找 ~~~C int Search_Seq(SSTable ST, KeyType key) { ST.R[0].key = key; // key值存入表头(哨兵) int i; for(i = ST.length; ST.R[i].key != key; --i); return i; } ~~~ 免去了查找过程中每一步都要检测整个表是否查找完毕 ASL = (n+1)/2 时间复杂度: O(n) #### 优点 对表结构无任何要求,适用于线性表的顺序存储结构、链式存储结构 #### 缺点 平均查找长度较大,查找效率较低,n很大时,不宜采用顺序查找 ### 折半查找 也称二分查找,查找效率较高,但要求线性表必须采用顺序存储结构,且表中元素按关键字有序排列 #### 查找过程 从表的中间记录开始,若给定值和中间记录的关键字相等,则查找成功;若大于或小于中间记录的关键字,则在表中大于或小于中间记录的那一半中查找,并重复操作,直到查找成功 用low和high表示当前查找区间的下界和上界,mid为区间的中间位置 #### 算法 ~~~C int Search_Bin(SSTable ST,KeyType key) { //若找到,则函数值为该元素在表中的位置,否则为0 low=1; high=ST.length; while(low<=high){ mid=(low+high)/2; if(key==ST.R[mid].key) return mid; else if(key<ST.R[mid].key) high=mid-1; //前一子表查找 else low=mid+1; //后一子表查找 } return 0; //表中不存在待查元素 } ~~~ 递归 ~~~C int Search_Bin (SSTable ST, keyType key, int low, int high) { if(low>high) return 0; //查找不到时返回0 mid=(low+high)/2; if(key==ST.elem[mid].key) return mid; else if(key<ST.elem[mid].key) Search_Bin(ST, key, low, mid-1) //递归 else Search_Bin(ST, key, mid+1, high) //递归 } ~~~ ASL=每一层结点数*深度之和/总结点数 查找成功时比较次数:d = [log$_{2}$n] + 1 #### 优点 比较次数少,查找效率高 时间复杂度O(log$_{2}$n) #### 缺点 对表结构要求高,只能用于顺序存储的有序表,查找前需排序,费时 不适于数据元素经常变动的线性表 ### 分块查找 索引顺序查找,性能介于顺序和折半查找之间 #### 查找过程 分成若干子表,每个子表中的数值都比后一块中数值小(子表中未必有序),构造索引表,由各子表中的最大关键字和起始地址(头指针)构成  * 对索引表进行顺序或折半查找(索引表有序) * 确定了待查关键字所在子表后,顺序查找(子表无序) #### 查找性能 ASL = L$_{b}$+L$_{w}$ L$_{b}$:索引表查找的ASL L$_{w}$:子表查找的ASL  s为每块内部的记录个数,n/s即块的数目 #### 优点 插入和删除比较容易,无需大量移动 #### 缺点 要增加一个索引表的存储空间并对初始索引表进行排序运算 适用于既要快速查找又经常变动的线性表 ### Fibonacci查找 #### 查找过程 根据Fibonacci数列特点对查找表分割 | | **顺序查找** | **折半查找** | **分块查找** | | -------------- | -------------------------------- | ------------------ | -------------------------------- | | **ASL** | **最大** | **最小** | **两者之间** | | **表结构** | **有序表、无序表** | **有序表** | **分块有序表** | | **存储结构** | **顺序存储结构** **线性链表** | **顺序存储结构** | **顺序存储结构** **线性链表** | ## 树表的查找 ### 二叉排序树 空树或具有下面性质的树 * 左子树不空,则左子树上的所有结点值小于它的根结点的值 * 右子树不空,则右子树上的所有结点值大于它的根结点的值 * 左、右子树也分别为二叉排序树 构造二叉排序树目的:提高查找和插入删除关键字的速度 中序遍历二叉排序树得到一个递增序列 #### 查找算法 * 二叉排序树为空,查找失败,返回空指针 * 非空,给定key值与根结点的关键字值比较 * =:查找成功,返回根结点地址 * <:查其左子树 * \>:查其右子树 * 递归实现 ~~~C BSTree SearchBST(BSTree T,KeyType key) { if((!T) || key==T->data.key) return T; else if (key<T->data.key) return SearchBST(T->lchild,key); //在左子树中继续查找 else return SearchBST(T->rchild,key); //在右子树中继续查找 } // SearchBST ~~~ #### 插入 * 先查找,已有不再插 * 没有,查找至某个叶子结点的左子树或右子树,插入成为左孩子或者右孩子(一定在叶结点上) #### 生成 一系列查找和插入实现 **不同插入次序的序列生成不同形态的二叉排序树** #### 删除 * 删除叶结点,双亲结点指向它后释放即可 * 被删除结点缺右子树,双亲结点指向它的左子女结点,释放它 * 被删除结点缺左子树,双亲结点指向它的右子女结点,释放它 * 被删结点左右子树均存在,此时可以用它的前驱节点或后继结点代替它,这样整体结构变化很小 #### 查找性能 平均查找长度和二叉树的形态有关 最好:log$_{2}$n(形态匀称,与二分查找的判定树相似) 最坏: (n+1)/2(单支树) 因此提出**平衡二叉树**(AVL树) ### 平衡二叉树 每一个结点的左子树和右子树的高度之多差绝对值小于等于1 #### 平衡因子BF 该结点左子树和右子树的高度差 ==》-1、0、1 #### 最小不平衡二叉树 距离插入结点最近的,且平衡因子的绝对值大于1的结点为根的子树,称其为最小不平衡二叉树 平衡二叉树实现即调整最小不平衡二叉树中各结点的链接关系,使之成为新的平衡子树 #### LL平衡旋转 顺时针旋转 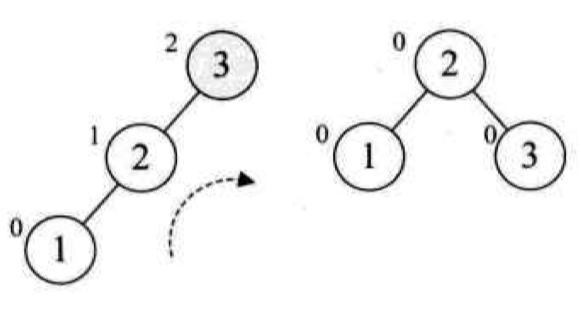 ~~~c void LL_rotate(BBSTNode *a) { BBSTNode *b; b=a->Lchild; a->Lchild=b->Rchild; b->Rchild=a; a->Bfactor=b->Bfactor=0; a=b; } ~~~ #### RR平衡旋转 逆时针旋转 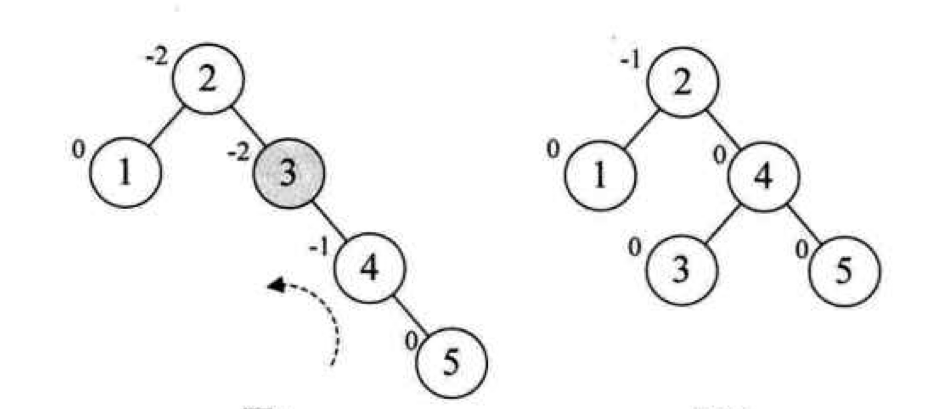 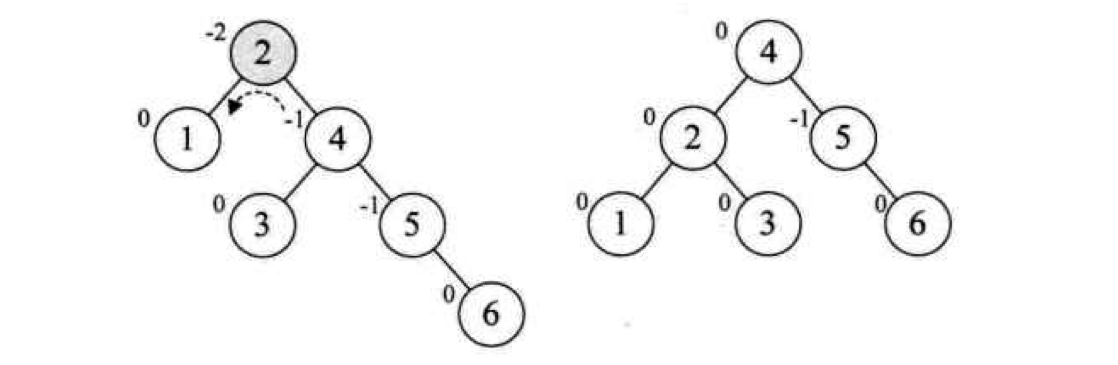 结点3本来是4的左孩子,由于旋转后需满足二叉排序树的特性,因此成了结点2的右孩子 ~~~C Void *RR_rotate(BBSTNode *a) { BBSTNode *b; b=a->Rchild; a->Rchild=b->Lchild; b->Lchild=a; a->Bfactor=b->Bfactor=0; a=b; } ~~~ #### RL平衡旋转 如下不能直接进行顺时针旋转  结点7的BF为-2,结点10的为1,一正一副,故不能直接旋转 应先将结点9和10顺时针旋转后再整体逆时针旋转  ~~~C Void RL_rotate(BBSTNode *a) { BBSTNode *b,*c ; b=a->Rchild; c=b->Lchild; /* 初始化 */ a->Rchild=c->Lchild; b->Lchild=c->Rchild; c->Lchild=a; c->Rchild=b; if (c->Bfactor==1) { a->Bfactor=0; b->Bfactor=-1; } else if (c->Bfactor==0) a->Bfactor=b->Bfactor=0; else { a->Bfactor=1; b->Bfactor=0; } } ~~~ #### LR平衡旋转 道理同RL一样 先逆时针旋转两个,再整体顺时针旋转 ~~~C void LR_rotate(BBSTNode *a) { BBSTNode *b,*c; b=a->Lchild; c=b->Rchild; /* 初始化 */ a->Lchild=c->Rchild; b->Rchild=c->Lchild; c->Lchild=b; c->Rchild=a; if (c->Bfactor==1) { a->Bfactor=-1; b->Bfactor=0; } else if (c->Bfactor==0) a->Bfactor=b->Bfactor=0; else { a->Bfactor=0; b->Bfactor=1; } } ~~~ #### 平衡二叉排序树的插入 * 判断插入结点后二叉排序树是否产生不平衡 * 找出失衡的最小子树 * 判断旋转类型,做出调整 ~~~C bool InsertAVL(BSTree &T, int e, bool &taller) {//插入结点 e if(!T){ //插入,树长高 T=(BSTree)malloc(sizeof(BSTNode)); T->data=e; T->lchild=NULL; T->rchild=NULL; T->bf=0; taller=TRUE; }else{ if(e == T->data){ //已存在 taller=FALSE; printf("已存在相同结点\n"); return 0; } if(T->data > e){ //左树中搜索 if(!InsertAVL(T->lchild,e,taller)){ return 0; //未插入 } if(taller){ switch(T->bf){ case 0: //等高 T->bf=1; taller=TRUE;break; case 1: //左高,左平衡 LeftBalance(T);taller=FALSE;break; case -1: //右高,现等高 T->bf=0;taller=FALSE;break; } } } else{ if(!InsertAVL(T->rchild,e,taller)){ return 0; } if(taller){ switch(T->bf){ case 0: T->bf=-1; taller=TRUE;break; case 1: T->bf=0;taller=FALSE;break; case -1: RightBalance(T);taller=FALSE;break; } } } } return 1; } void LeftBalance(BSTree &T){ //对以指针T所指结点为根的二叉树作左平衡旋转处理 lc=T->lchild; switch(lc->bf){ case 1: //插在T左孩的左树,右旋 T->bf=lc->bf=0; R_Rotate(T); break; case -1: //插在T左孩的右树,双旋 rd=lc->rchild; switch(rd->bf){ //修改T及左孩平衡因子 case 1: T->bf=-1;lc->bf=0;break; case 0: T->bf=lc->bf=0;break; case -1: T->bf=0;lc->bf=1;break; } rd->bf=0; L_Rotate(T->lchild); R_Rotate(T); } } ~~~ ### 多路查找树 每个结点的孩子数可以多于两个,且每一个结点可以存储多个元素 #### B-树 m阶B-树(m≥3) * 每个结点分指数≤m * 根结点分支数≥2 * 其余分支结点的分支数≥[m/2] * 所有叶子结点在同一层,不带信息,成为失败结点 具体内容看课本 ## 哈希表的查找 [【数据结构与算法】详解什么是哈希表,并用代码手动实现一个哈希表_零一的博客-CSDN博客](https://blog.csdn.net/l_ppp/article/details/107536781?ops_request_misc=%7B%22request%5Fid%22%3A%22163853456416780264061513%22%2C%22scm%22%3A%2220140713.130102334..%22%7D&request_id=163853456416780264061513&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~top_positive~default-1-107536781.pc_search_mgc_flag&utm_term=哈希表数据结构&spm=1018.2226.3001.4187) ### 定义 记录的存储位置与关键字之间存在对应关系-->哈希函数实现 优点:查找速度极快,查找效率和元素个数n无关 哈希方法:选取某个函数,依该函数按关键字计算元素的存储位置,并按此存放;查找时,由同一个函数对给定值k计算地址,将k与地址单元中元素关键码进行比,确定查找是否成功。 冲突:不同的关键码映射到同一个哈希地址 eg:  key1 ≠ key2 但H(key1)=H(key2) 同义词:具有相同函数值的两个关键字 ### 减少冲突 * 构造好的哈希函数 * 制定一个好的解决冲突方案 #### 直接定址法 Hash(key) = a×key + b (a、b为常数) ##### 优点 以关键码key的某个线性函数值为哈希地址,不会产生冲突 ##### 缺点 要占用连续的地址空间,空间效率低 #### 数字分析法 对关键字进行分析,取关键字的若干位或组合作为哈希地址(如学号、编码之类的) #### 平方取中法 将关键字平方后去中间几位作为哈希地址 #### 折叠法 将关键字分割成位数相同的几部分(最后一部分可以不同),然后取这几部分的叠加和作为哈希地址 数位叠加: * 移位叠加:将分割后的几部分低位对齐相加 * 间界叠加:从一段到另一端沿分割界来回折叠,然后对齐相加 适用于关键字位数很多,且每一位上数字分布大致均匀的情况 #### *除留余数法*(更优) Hash(key)=key mod p (p是一个整数) 设表长m * 选取p≤m且为质数 * 选取p=2$^{i}$(p≤m):运算便于用移位来实现,但等于将关键字的高位忽略而仅留下低位二进制数,高位不同而低位相同的关键字是同义词 * 选取p=q×f(q、f都是质因数,p≤m):则所有含有q或f因子的关键字的散列地址均是q或f的倍数 #### 随机数法 ### 构造哈希函数考虑因素 * 执行速度 * 关键字的长度 * 哈希表的大小 * 关键字的分布情况 * 查找效率 ### 处理冲突 #### 开放定址法 有冲突时就去寻找下一个空的哈希地址,只要哈希表足够大,总能存下 ##### 线性探测法 H~i~ = (Hash(key) + d$_{i}$ ) mod m ( 1≤i < m ) 其中:m为哈希表长度 d$_{i}$为增量序列 1,2,…m-1,且d$_{i}$ = i eg:  优点:总能放下 缺点:产生聚集现象,降低查找效率 ##### 二次探测法 解决线性探测法聚集缺点 H~i~ = (Hash(key) ± d~i~ ) mod m ( 1≤i < m ) 其中:m为哈希表长度,m要求是某个4k+3的质数; d~i~为增量序列 1$^{2}$,-1$^{2}$,2$^{2}$,-2$^{2}$,…,q$^{2}$ 仍是上面的例子  ##### 伪随机数探测法 H$_{i}$ = (Hash(key) + d$_{i}$ ) mod m ( 1≤i < m ) 其中:m为哈希表长度 d$_{i}$为随机数 step1 取数据元素的关键字key,计算其哈希函数值(地址)。若该地址对应的存储 空间还没有被占用,则将该元素存入;否则执行step2解决冲突 step2 根据选择的冲突处理方法,计算关键字key的下一个存储地址。若下一个存储地址仍被占用,则继续执行step2,直到找到能用的存储地址为止 #### 链地址法(更优) 相同哈希地址的记录链成一单链表,m个哈希地址就设m个单链表,然后用用一个数组将m个单链表的表头指针存储起来,形成一个动态的结构 step1 取数据元素的关键字key,计算其哈希函数值(地址)。若该地址对应的链表为空,则将该元素插入此链表;否则执行step2解决冲突 step2 根据选择的冲突处理方法,计算关键字key的下一个存储地址。若该地址对应的链表为不为空,则利用链表的前插法或后插法将该元素插入此链表 优点 * 非同义词不会冲突,无聚集现象 * 链表上结点空间动态申请,更适合于表长不确定的情况 eg:关键字(19,14,23,1,68,20,84,27,55,11,10,79)  ### ASL衡量查找算法 取决因素 * 哈希函数 * 处理冲突的方法 * 哈希表的装填因子α α=表中填入的记录数/哈希表长度,越大,表中记录数越多,发生冲突可能性越大,查找时对比的次数就越多 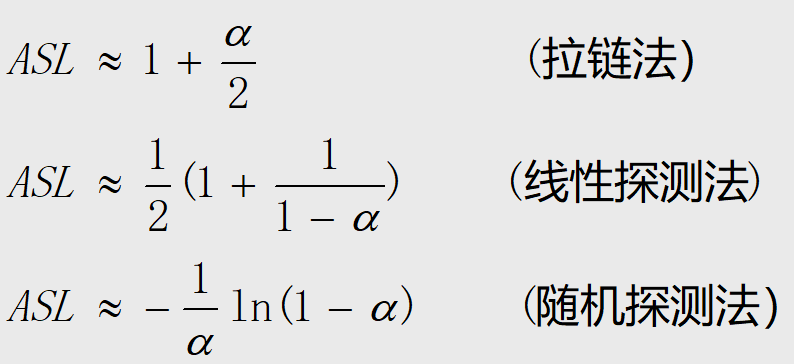 最后修改:2021 年 12 月 12 日 © 允许规范转载 打赏 赞赏作者 支付宝微信 赞 如果觉得我的文章对你有用,请随意赞赏