机器学习1
前言
应用:
- 数据库挖掘:web数据点击、医疗记录、生物、工程
- 无法手动编程的程序:手写识别、NLP(自然语言处理)、计算机视觉
- 自适应程序:Netflix产品推荐等
定义:
- 使计算机自学习
- 从E经验中学习,执行T任务,得出性能衡量P,看是否提高了经验E
监督学习(supervised learning)
eg:直线还是二次函数拟合数据模型?给出预测答案
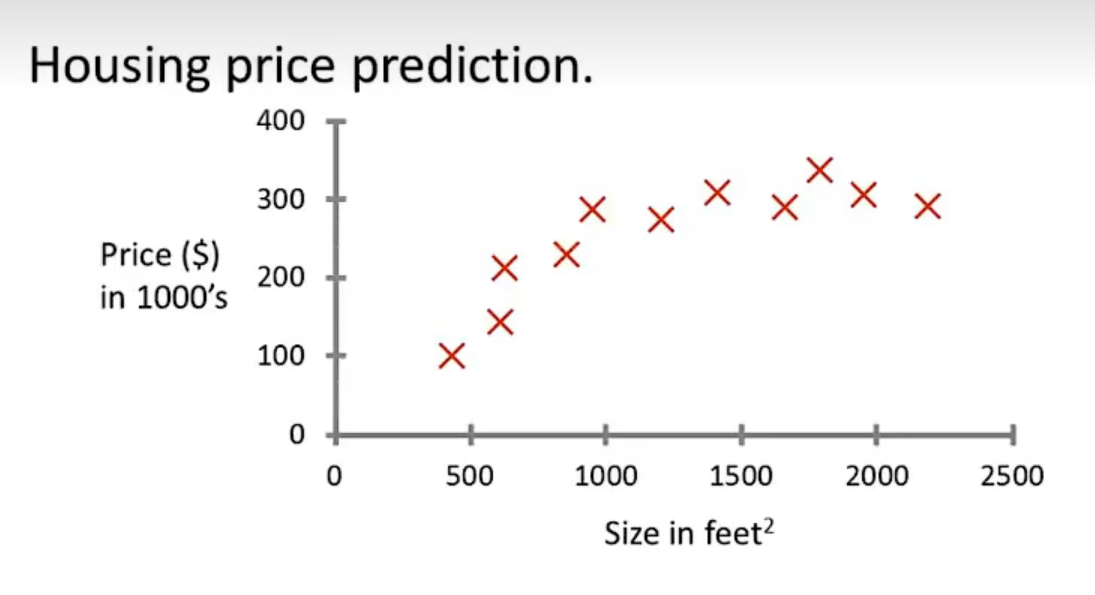
回归问题:预测值为多少?(房价)
分类问题:归为哪类?(预测肿瘤良性还是恶行)
无监督学习(unsupervised learning)
聚类算法(clustering):谷歌新闻从不同网站获取同一个新闻、DNA包含特定基因的程度、组织计算机集群(协同工作的放一起)、社交网络分析(QQ可能想认识的好友之类的)、市场分割(细分)、天文数据分析
不能给出具体的结果答案
模型描述
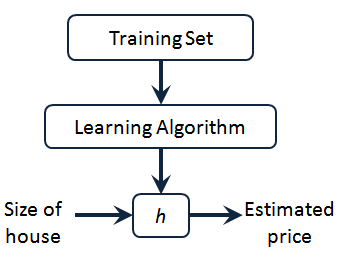
h代表假设函数,x$\rightarrow$y
代价函数
$h_{\theta}(x) = \theta_{0} + \theta_{1}x$,怎么选择θ0、θ1?
代价函数如下,也被称作平方误差函数,要想得到最好结果尽可能让下面值变小
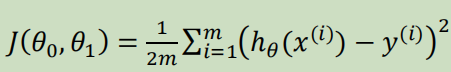
即尽可能$minJ(\theta_{0},\theta_{1})$
在三维空间中,存在某个$(\theta_{0},\theta_{1})$使得最小
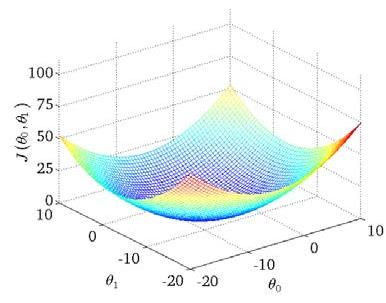
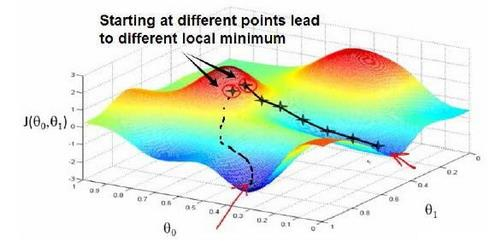
梯度下降(gradient descent)
求函数最小值的方法
批量梯度下降算法公式:

α是学习率,更新要在最后做(同步更新)
梯度下降的线性回归
结合两者:

得到偏导数后代入梯度下降:
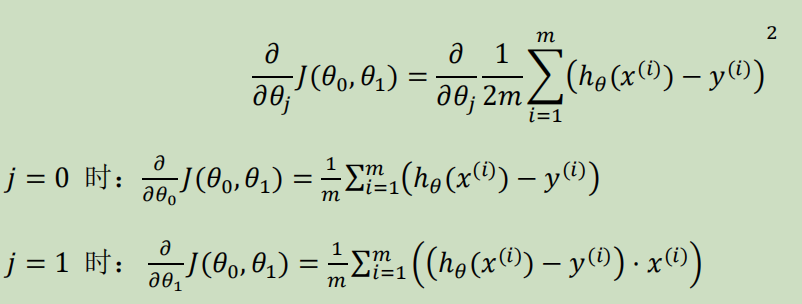
线性代数回顾
我们一般在 OCTAVE 或者 MATLAB 中进行计算矩阵的逆矩阵($AA^{-1}=I,I是单位矩阵,A是方阵$)
矩阵的转置:m*n→n*m,$A^T=B$
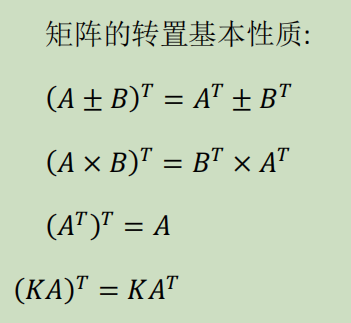
多变量线性回归
对房价模型增加更多的特征,例如房间数楼层等,构成一个含有多个变量的模型,模型中的特征为(x0, x1, . . . , xn)
- n代表特征的数量
- $x^{(i)}$代表第i个训练实例(向量)
- $x_{j}^{(i)}$代表第i行第j个特征值
eg:新的假设函数为$h_{\theta}(x)=\theta_0x_0+\theta_1x_2+……+\theta_nx_n$(x0为1),模型的参数为n+1维向量,训练实例也是n+1维向量
此时$h_{\theta}(x)=\theta^TX$
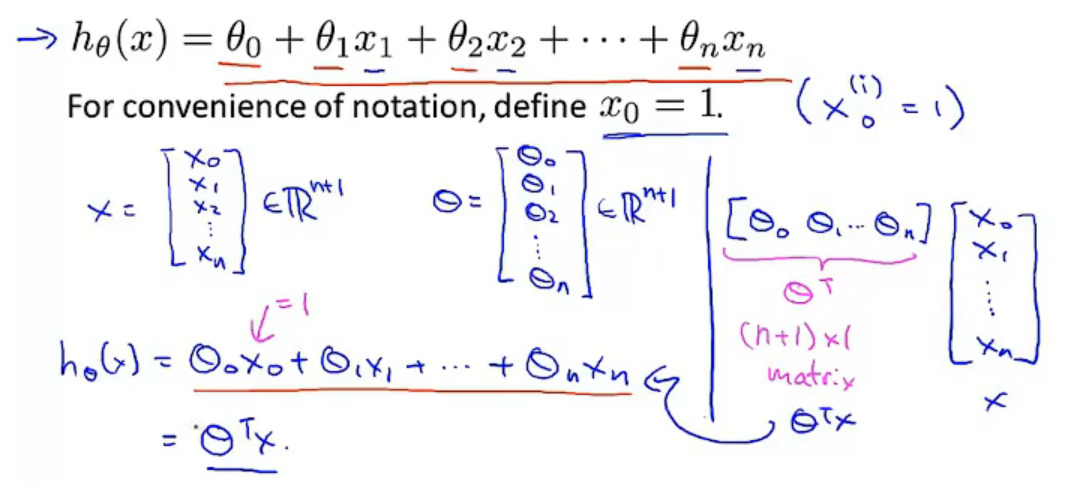
多元梯度下降法
hθ为上面的假设函数
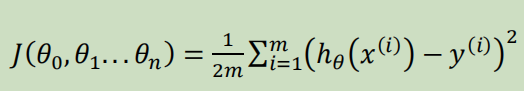
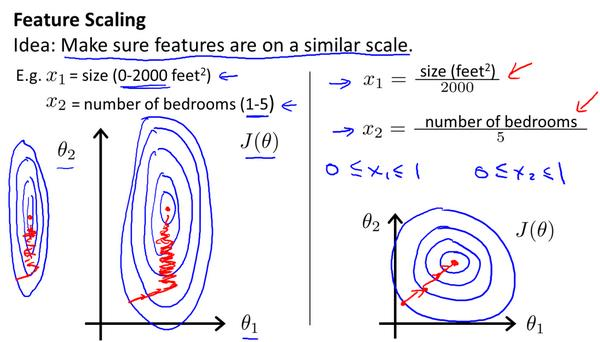
特征缩放
将特征的取值约束到-1到1的范围,减少迭代次数
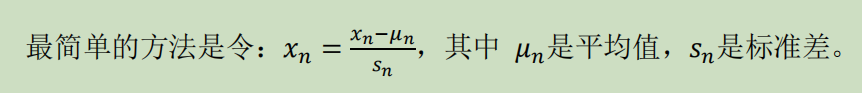
学习率
每步迭代后 $J(\theta)$ 应该都减小; 自动收敛测试?eg:$\varepsilon<10^{-3}$
如果学习率α过小,则达到收敛所需的迭代次数会非常高;如果学习率α过大,每次迭代可能不会减小代价函数,可能会越过局部最
小值导致无法收敛
特征和多项式回归
有时候直线拟合数据不是很好,用多项式(二次、三次甚至更多)

正规方程
区别于迭代求值,是通过直接求解方程得到结果
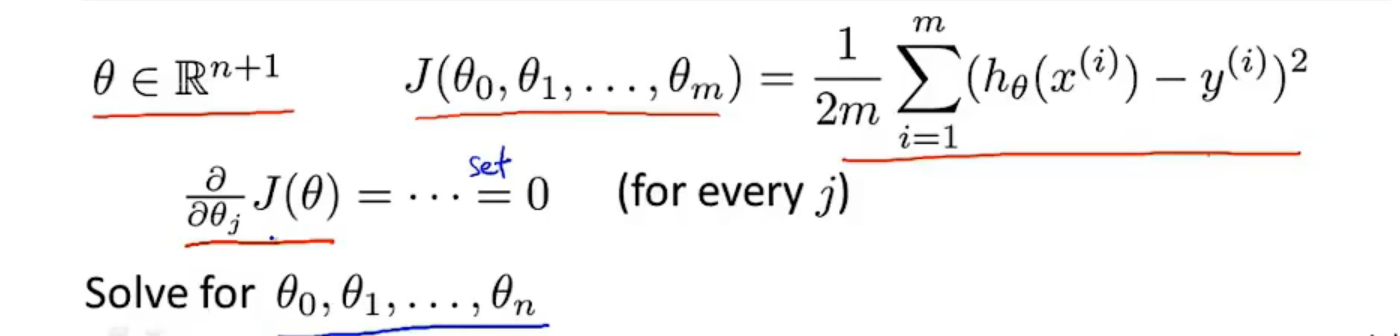
假设训练集特征矩阵为X(包含了x0=1),训练结果为向量y,则正规方程解得$\theta=(X^TX)^{-1}X^Ty$
正规方程 vs 梯度下降
| 梯度下降 | 正规方程 |
|---|---|
| 需要选择学习率α | 不需要 |
| 需要多次迭代 | 一次运算得出 |
| 当特征数量n很大时也能较好适用(大于10^6时就开始考虑该方法吧) | 需要计算复杂矩阵,运算代价大 |
| 适用于各种类型的模型 | 只适用于线性模型,不适合逻辑回归模型等其他模型 |
Octave:求解正规方程:pinv(X'*X)*X'*y(伪逆)
$X^TX$为奇异矩阵(不可逆):删除冗余特征或者正规化特征,解决不可逆问题
逻辑回归
分类
正确或错误?不适合使用线性回归,输出值可能小于0或大于1
假设陈述
$h_{\theta}(x)=g(\theta^TX)$代入$g(z)=\frac{1}{1+e^{-z}}$
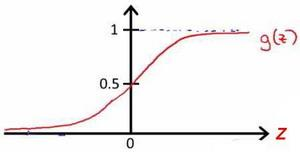
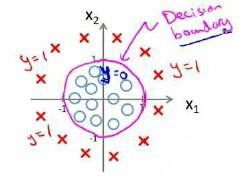
决策界限
由上图:$\theta^TX\ge0$,预测y=1;$\theta^TX\lt0$,预测y=0;

蓝线即为决策界限,但也会有无法直接线性拟合数据的情况