机试day9

博主： Xherlock
发布时间：2023 年 06 月 18 日
321 次浏览
暂无评论
2434字数
分类： C/C++&机试

# 机试day9

## 鸡兔同笼

**描述**

一个笼子里面关了鸡和兔子（鸡有2只脚，兔子有4只脚，没有例外）。已经知道了笼子里面脚的总数a，问笼子里面至少有多少只动物，至多有多少只动物。

**输入描述**：

每组测试数据占1行，每行一个正整数a (a < 32768)

**输出描述**：

输出包含n行，每行对应一个输入,包含两个正整数，第一个是最少的动物数，第二个是最多的动物数，两个正整数用一个空格分开 如果没有满足要求的答案，则输出两个0。

思路：最少时要么全是兔子要么1只鸡剩下全是兔子；最多时全是鸡。出现奇数说明不满足

~~~c++
#include <iostream>
using namespace std;

int main() {
    int a;
    while (cin >> a) {
        int min = 0, max = 0;
        if (a % 2 == 0) {
            min = a / 4 + a % 4 / 2;
            max = a / 2;
        }
        cout << min << " " << max << endl;
    }
}
~~~

## 代理服务器

[代理服务器_牛客题霸_牛客网 (nowcoder.com)](https://www.nowcoder.com/practice/1284469ee94a4762848816a42281a9e0?tpId=60&tqId=29476&tPage=1&ru=/kaoyan/retest/1001&qru=/ta/tsing-kaoyan/question-ranking)

**描述**

使用代理服务器能够在一定程度上隐藏客户端信息，从而保护用户在互联网上的隐私。我们知道n个代理服务器的IP地址，现在要用它们去访问m个服务器。这 m 个服务器的 IP 地址和访问顺序也已经给出。系统在同一时刻只能使用一个代理服务器，并要求不能用代理服务器去访问和它 IP地址相同的服务器（不然客户端信息很有可能就会被泄露）。在这样的条件下，找到一种使用代理服务器的方案，使得代理服务器**切换的次数尽可能得少**。

**输入描述**：

每个测试数据包括 n + m + 2 行。   第 1 行只包含一个整数 n，表示代理服务器的个数。   第 2行至第n + 1行每行是一个字符串，表示代理服务器的 IP地址。这n个 IP地址两两不相同。   第 n + 2 行只包含一个整数 m，表示要访问的服务器的个数。   第 n + 3 行至第 n + m + 2 行每行是一个字符串，表示要访问的服务器的 IP 地址，按照访问的顺序给出。   每个字符串都是合法的IP地址，形式为“xxx.yyy.zzz.www”，其中任何一部分均是0–255之间的整数。输入数据的任何一行都不包含空格字符。    其中，1<=n<=1000，1<=m<=5000。

**输出描述**：

可能有多组测试数据，对于每组输入数据， 输出数据只有一行，包含一个整数s，表示按照要求访问服务器的过程中切换代理服务器的最少次数。第一次使用的代理服务器不计入切换次数中。若没有符合要求的安排方式，则输出-1。

~~~
输入：
3
166.111.4.100
162.105.131.113
202.112.128.69
6
72.14.235.104
166.111.4.100
207.46.19.190
202.112.128.69
162.105.131.113
118.214.226.52
输出：
1
~~~

思路：这题真的好烧脑啊啊啊啊啊啊，但我做出来了啊啊啊啊啊啊

本题的贪心策略体现在尽可能是连续多个被访问的服务器IP地址都不和代理服务器IP相同，思路逆向来说就是找到最后一个代理服务器前，其他代理服务器均和已访问过的服务器IP地址相匹配。

结合测试案例分析来说：在访问第五个服务器时（162.105.131.113），它的IP地址和其中一个代理服务器IP相同，但是另外两个都已在先前访问过，此时162.105.131.113这个IP的代理服务器是最晚出现的（最贪心的），因此改变次数+1

~~~c++
#include <cstring>
#include <iostream>
using namespace std;

int main() {
    int n, m;
    while (cin >> n) {
        // 输入代理服务器IP
        string proxy_s[n];
        for (int i = 0; i < n; i++) {
            cin >> proxy_s[i];
        }  
        // 输入访问服务器IP
        cin >> m;
        string access_s[m];
        for (int i = 0; i < m; i++) {
            cin >> access_s[i];
        }
        // 定义bool类型数组，true表示改代理服务器被访问过；初始化全为false
        bool is_accessed[n];
        memset(is_accessed, false, sizeof(is_accessed));
        int result = 0, access_n = n;	// result是改变代理服务器的次数，access_n表示还未被访问过的代理服务器数目，初始为n
        // 遍历要访问的服务器IP，和代理服务器IP比较
        for (int i = 0; i < m; i++) {
            int j = 0;	// 记录下来哪个代理服务器IP被匹配了
            for (; j < n; j++) {
                if (access_s[i] == proxy_s[j] && !is_accessed[j]) {	// IP匹配且该代理服务器之前没被访问过
                    is_accessed[j] = true;	// 该代理服务器已被访问
                    access_n--;	//还未被访问过的代理服务器数目-1
                    break;		// 直接退出比较，以记录下该代理服务器下标
                }
            }
            if (!access_n) {	// 如果所有的代理服务器均已被访问，表示需要换一次代理，result++
                if (n == 1) {	// 特殊情况，只有一个代理服务器，且还被匹配了，直接输出-1
                    result = -1;
                    break;
                }
                result++;
                access_n = n - 1;	// 当前还在使用代理服务器，因此未被访问过的代理服务器数目应为n-1
                memset(is_accessed, false, sizeof(is_accessed));	// 全置false
                is_accessed[j] = true;	// 当前的代理服务器设置为true
            }
        }
        cout << result << endl;
    }
}
~~~

memset要善用，虽然容易写错（溢出之类的？），但是不需要循环初始化值，很方便

看了下其他人的解题思路，发现有用二分法（先sort代理服务器IP）加快匹配的，也行，不过既然能pass了，那就没必要再多此一举了

## To Fill or Not to Fill

**描述**

With highways available, driving a car from Hangzhou to any other city is easy. But since the tank capacity of a car is limited, we have to find gas stations on the way from time to time. Different gas station may give different price. You are asked to carefully design the cheapest route to go.

**输入描述**：

For each case, the first line contains 4 positive numbers: Cmax (<= 100), the maximum capacity of the tank; D (<=30000), the distance between Hangzhou and the destination city; Davg (<=20), the average distance per unit gas that the car can run; and N (<= 500), the total number of gas stations. Then N lines follow, each contains a pair of non-negative numbers: Pi, the unit gas price, and Di (<=D), the distance between this station and Hangzhou, for i=1,...N. All the numbers in a line are separated by a space.

**输出描述**：

For each test case, print the cheapest price in a line, accurate up to 2 decimal places. It is assumed that the tank is empty at the beginning. If it is impossible to reach the destination, print "The maximum travel distance = X" where X is the maximum possible distance the car can run, accurate up to 2 decimal places.

思路：本人除了会写结构体、排序、写输入输出，对于算法设计完全是懵逼的，看了其他人思路只能自叹不如

正确做法是将每个距离设置一个bool变量，即bool数组，走过即设置为true；贪婪策略需要我们以最小油价走最长距离，因此排序按照油价排，从最小的装满油箱开始走，直到走完最长距离或者到达终点

~~~c++
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;

struct GasStation {
    double price;
    int distance;
};

bool stationCompare(GasStation x, GasStation y) {
    return x.price < y.price;
}

int main() {
    int Cmax, D, Davg, N;
    while (cin >> Cmax >> D >> Davg >> N) {
        GasStation S[N];
        bool tag[D+1];
        memset(tag, false, sizeof(tag));
        for (int i = 0; i < N; i++) {
            cin >> S[i].price >> S[i].distance;
        }
        sort(S, S+N, stationCompare);
        double total_price = 0;
        for (int i = 0; i< N; i++) {
            int currentdistance = 0;
            for (int j = S[i].distance + 1; j <= S[i].distance + Cmax * Davg; j++) {
                if (!tag[j]) {
                    tag[j] = true;
                    currentdistance++;
                }
                if (j == D || j == S[i].distance + Cmax * Davg) {
                    total_price += S[i].price * currentdistance / (Davg * 1.0);
                    break;
                }
            }
        }
        int fill = 1;
        double max_distance = 0;
        for (int i = 1; i <= D; i++) {
            if (!tag[i]) {
                fill = 0;
                break;
            } else
                max_distance++;
        }
        if (fill)
            printf("%.2f\n", total_price);
        else
            printf("The maximum travel distance = %.2f\n", max_distance);
    }
}
~~~

## n的阶乘

使用递归实现

~~~c++
#include <iostream>
using namespace std;

long long Factorial(int n) {
    if (n == 0)
        return 1;
    else
        return n * Factorial(n-1);
}

int main() {
    int n;
    while (cin >> n) {
        cout << Factorial(n) << endl;
    }
}
~~~

### 杨辉三角形

打印某一行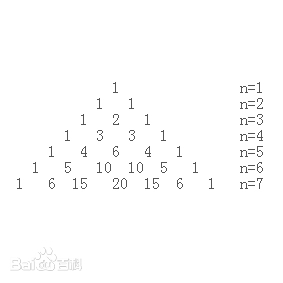

![format,f_auto.jpeg](http://xherlock.top/usr/uploads/2023/06/4009197352.jpeg)

~~~c++
#include <iostream>
using namespace std;

int Yanghui(int n, int i) {
    if (i == 0 || n == i + 1)
        return 1;
    else
        return Yanghui(n-1, i-1) + Yanghui(n-1, i);
}

int main() {
    int n;
    while (cin >> n) {
        for (int i = 0; i < n; i++) {
            cout << Yanghui(n, i);
            if (i != n -1)
                cout << " ";
        }
    }
}
~~~

### 全排列

[全排列_牛客题霸_牛客网 (nowcoder.com)](https://www.nowcoder.com/practice/5632c23d0d654aecbc9315d1720421c1?tpId=61&tqId=29515&tPage=1&ru=/kaoyan/retest/1002&qru=/ta/pku-kaoyan/question-ranking)

**描述**

给定一个由不同的小写字母组成的字符串，输出这个字符串的所有全排列。 我们假设对于小写字母有'a' < 'b' < ... < 'y' < 'z'，而且给定的字符串中的字母已经按照从小到大的顺序排列。

**输入描述**：

输入只有一行，是一个由不同的小写字母组成的字符串，已知字符串的长度在1到6之间。

**输出描述**：

输出这个字符串的所有排列方式，每行一个排列。要求字母序比较小的排列在前面。字母序如下定义： 已知S = s1s2...sk , T = t1t2...tk，则S < T 等价于，存在p (1 <= p <= k)，使得 s1 = t1, s2 = t2, ..., sp - 1 = tp - 1, sp < tp成立。 每组样例输出结束后要再输出一个回车。

思路：最简单的直接STL（标准库）里algorithm的next_permutation

正常思路：递归

~~~c++
#include <iostream>
#include <algorithm>
using namespace std;
string str;

void swap(int x, int y) {
    char tmp = str[x];
    str[x] = str[y];
    str[y] = tmp;
}

void func(int i, int j) {
    if (i == j)
        cout << str << endl;
    else {
        for (int m = i; m < str.size(); m++) {
            string s = str;
            swap(i, m);
            sort(str.begin() + i + 1, str.end());
            func(i+1, j);
            str = s;
        }
    }
}

int main() {
    while (cin >> str) {
        sort(str.begin(), str.end());
        func(0, str.size()-1);
    }
}
~~~

### Fibonacci

求第n个Fibonacci数，思路就是递归（分而治之）

~~~c++
#include <iostream>
using namespace std;

int Fibonacci(int n) {
    if (n == 0)
        return 0;
    else if (n == 1)
        return 1;
    else
        return Fibonacci(n-1) + Fibonacci(n-2);
}

int main() {
    int n;
    while (cin >> n) {
        cout << Fibonacci(n) << endl;
    }
}
~~~

### 二叉树

[二叉树_牛客题霸_牛客网 (nowcoder.com)](https://www.nowcoder.com/practice/f74c7506538b44399f2849eba2f050b5?tpId=61&tqId=29557&tPage=3&ru=/kaoyan/retest/1002&qru=/ta/pku-kaoyan/question-ranking)

**描述**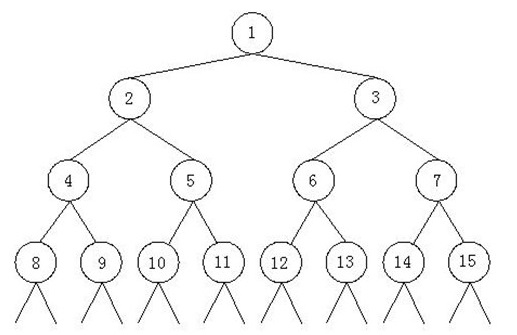

![39_1429598902788_btree.jpg](http://xherlock.top/usr/uploads/2023/06/2564805606.jpg)

如上所示，由正整数1，2，3……组成了一颗特殊二叉树。我们已知这个二叉树的最后一个结点是n。现在的问题是，结点m所在的子树中一共包括多少个结点。   比如，n = 12，m = 3那么上图中的结点13，14，15以及后面的结点都是不存在的，结点m所在子树中包括的结点有3，6，7，12，因此结点m的所在子树中共有4个结点。

**输入描述**：

输入数据包括多行，每行给出一组测试数据，包括两个整数m，n (1 <= m <= n <= 1000000000)。

**输出描述**：

对于每一组测试数据，输出一行，该行包含一个整数，给出结点m所在子树中包括的结点的数目。

~~~
输入：
3 12
0 0
输出：
4
~~~

思路：分别求左子树和右子树节点个数【分治法】

~~~c++
#include <iostream>
using namespace std;

int get_children(int m, int n) {
    if (m <= n)
        return 1 + get_children(2 * m, n) + get_children(2 * m + 1, n);
    else
        return 0;
}

int main() {
    int m, n;
    while (cin >> m >> n) {
        if (m == 0)
            break;
        cout << get_children(m, n) << endl;
    }
}
~~~

## 2的幂次方

[2的幂次方_牛客题霸_牛客网 (nowcoder.com)](https://www.nowcoder.com/practice/7cf7b0706d7e4b439481f53e5fdac6e7?tpId=62&tqId=29460&tPage=1&ru=/kaoyan/retest/2002&qru=/ta/sju-kaoyan/question-ranking)

**描述**

Every positive number can be presented by the exponential form.For example, 137 = 2^7 + 2^3 + 2^0。   Let's present a^b by the form a(b).Then 137 is presented by 2(7)+2(3)+2(0). Since 7 = 2^2 + 2 + 2^0 and 3 = 2 + 2^0 , 137 is finally presented by 2(2(2)+2 +2(0))+2(2+2(0))+2(0).    Given a positive number n,your task is to present n with the exponential form which only contains the digits 0 and 2.

**输入描述**：

For each case, the input file contains a positive integer n (n<=20000).

**输出描述**：

For each case, you should output the exponential form of n an a single line.Note that,there should not be any additional white spaces in the line.

思路：需要先用while循环不断除2求出指数，在递归求指数的2次幂表示；其中如果指数为0或1的，直接s拼接即可

~~~c++
#include <iostream>
#include <vector>
using namespace std;

string func(int n) {
    string s;
    vector<int> exp;
    int i = 0;
    while (n != 0) {
        if (n % 2 == 1)
            exp.push_back(i);	// vector中添加指数值
        n /= 2;
        i++;
    }
    for (int j = exp.size() - 1; j >= 0; j--) {
        if (exp[j] == 0)		// 指数为0直接+2的0次方
            s += "2(0)";
        else if (exp[j] == 1)	// 指数为1直接+2
            s += "2";
        else
            s += "2(" + func(exp[j]) + ")";
        if (j != 0)				// 除了最后一个都添加一个加号
            s += "+";
    }
    return s;
}

int main() {
    int n;
    while (cin >> n) {
        cout << func(n) << endl;
    }
}
~~~

## Catch That Cow

题目大意：给定农夫位置N，奶牛K，农夫可以行走：1min从X到X-1或X+1；传送：1min从X到2X，问需要最少时间抓到奶牛

思路：使用BFS（宽度优先搜索），从搜索起点开始，不断优先访问当前节点邻居，然后按照访问邻居的顺序去访问每个邻居的所有邻居（已访问的除外）

对于本题来说，可以设置二元组状态(n, t)，从(n, t)到下一分钟可能转为三种状态(n-1, t+1)、(n+1, t+1)、(2n, t+1)，因此可使用BFS不断扩展，直到第一次访问到奶牛位置

~~~c++
#include <iostream>
#include <cstring>
#include <cstdio>
#include <queue>

using namespace std;

const int MAXN = 100001;

struct Status {
    int n, t;
    Status(int n, int t): n(n), t(t) {}
};

bool visit[MAXN];
int BFS(int n, int k) {
    queue<Status> myQueue;
    myQueue.push(Status(n, 0));
    visit[n] = true;
    while (!myQueue.empty()) {
        Status current = myQueue.front();
        myQueue.pop();
        if (current.n == k)
            return current.t;
        for (int i = 0; i < 3; i++) {
            Status next(current.n, current.t + 1);
            if (i == 0) 
                next.n += 1;
            else if (i == 1)
                next.n -= 1;
            else if (i == 2)
                next.n *= 2;
            if (next.n < 0 || next.n > MAXN || visit[next.n])
                continue;
            myQueue.push(next);
            visit[next.n] = true;
        }
    }
}
int main() {
    int n, k;
    cin >> n >> k;
    memset(visit, false, sizeof(visit));
    cout << BFS(n, k);
    return 0;
}
~~~

## Find The Multiple

给出一个正整数n，找到n的倍数m，使得m的十进制只包含0和1两种数字

思路：BFS找，此处不用担心被访问过的，因为数字始终增大，每次找10\*i、10\*i+1，这样保证了所有数均含0、1

~~~c++
#include <iostream>
#include <cstring>
#include <queue>

using namespace std;

int BFS_search(int n) {
    long long i = 1;
    queue<long long> myQueue;
    myQueue.push(i);
    while (!myQueue.empty()) {
        i = myQueue.front();
        myQueue.pop();
        if (i % n == 0)
            return i;
        myQueue.push(10 * i);
        myQueue.push(10 * i + 1);
    }
}

int main() {
    int n;
    while (cin >> n) {
        if (n == 0)
            break;
        cout << BFS_search(n) << endl;
    }
    return 0;
}
~~~

小结：

* BFS：搜索求解最优解问题
* DFS：查找问题是否有解

### A Knight's Journey

![IMG_20230617_201320.jpg](http://xherlock.top/usr/uploads/2023/06/1340343705.jpg)

思路：使用DFS从A1开始遍历，需要使用递归

这里需要理解题意：pxq，行是字母，列是数字，如上图我写了个简单的格式。对于字典序，字母小的先访问，然后数字小的先访问

~~~c++
#include <iostream>
#include <cstdio>
#include <string>
#include <cstring>

using namespace std;

const int MAXN = 30;
int p, q;
bool visit[MAXN][MAXN];
int direction[8][2] = {
    {-1, -2}, {1, -2}, {-2, -1}, {2, -1}, {-2, 1}, {2, 1}, {-1, 2}, {1, 2}
};

bool DFS(int x, int y, int step, string ans) {
    if (step == p * q) {
        cout << ans << endl << endl;
        return true;
    } else {
        for (int i = 0; i < 8; i++) {
            int nx = x + direction[i][0];
            int ny = y + direction[i][1];
            char col = ny + 'A';
            char row = nx + '1';
            if (nx < 0 || nx >= p || ny < 0 || ny >= q || visit[nx][ny]) 
                continue;
            visit[nx][ny] = true;
            if (DFS(x, y, step+1, ans + col + row))
                return true;
            visit[nx][ny] = false;
        }
    }
    return false;
}

int main() {
    int n;
    cin >> n;
    int casenumber = 0;
    while (n--) {
        cin >> p >> q;
        memset(visit, false, sizeof(visit));
        cout << "Scenario #" << ++casenumber << ":" << endl;
        visit[0][0] = true;
        if (!DFS(0, 0, 1, "A1")) 
            cout << "impossible" << endl << endl;
    }
    return 0;
}
~~~

## Square

题目：木棍拼正方形

~~~
输入：
3
4 1 1 1 1 
5 10 20 30 40 50
8 1 7 2 6 3 5 4 4
输出：
yes
no
yes
~~~

思路：三元组(sum, number, position)，sum表示当前拼凑的木棍总长，number表示已经拼凑成边长的数量，position表示当前木棍的编号

首先要按照从大到小排序木棍长度，一个边一个边的拼凑

~~~c++
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>

using namespace std;

const int MAXN = 25;
int side;
int m;
int sticks[MAXN];
bool visit[MAXN];

bool DFS(int sum, int number, int position) {
    if (number == 3)	// 剩下的绝对可以凑
        return true;
    int sample = 0;
    for (int i = position; i < m; i++) {
        if (visit[i] || sum + sticks[i] > side || sticks[i] == sample) // 加起来超过边长跳过，之前已经试过不可以的跳过（sample接收）
            continue;
        visit[i] = true;
        if (sum + sticks[i] == side) {	//直接开始下一条边
            if (DFS(0, number + 1, 0))
                return true;
            else  
                sample = sticks[i];
        } else {
            if (DFS(sum + sticks[i], number, i + 1))	// 接着拼凑
                return true;
            else
                sample = sticks[i];
        }
        visit[i] = false;
    }
    return false;
}

bool Compare(int x, int y) {
    return x > y;
}

int main() {
    int N;
    cin >> N;
    while (N--) {
        cin >> m;
        int len = 0;
        for (int i = 0; i < m; i++) {
            cin >> sticks[i];
            len += sticks[i];
        }
        if (len % 4 != 0)	// 不能被4整除，直接no
            cout << "no" << endl;
        memset(visit, false, sizeof(visit));
        sort(sticks, sticks+m, Compare);
        side = len / 4;
        if (sticks[0] > side)	// 最长木棍超出边长，直接no
            cout << "no" << endl;
        if (DFS(0, 0, 0))
            cout << "yes" << endl;
        else
            cout << "no" << endl;
    }
    return 0;
}
~~~

## 神奇的口袋

[神奇的口袋_牛客题霸_牛客网 (nowcoder.com)](https://www.nowcoder.com/practice/9aaea0b82623466a8b29a9f1a00b5d35?tpId=61&tqId=29531&tPage=2&ru=/kaoyan/retest/1002&qru=/ta/pku-kaoyan/question-ranking)

**描述**

有一个神奇的口袋，总的容积是40，用这个口袋可以变出一些物品，这些物品的总体积必须是40。John现在有n个想要得到的物品，每个物品的体积分别是a1，a2……an。John可以从这些物品中选择一些，如果选出的物体的总体积是40，那么利用这个神奇的口袋，John就可以得到这些物品。现在的问题是，John有多少种不同的选择物品的方式。

**输入描述**：

输入的第一行是正整数n (1 <= n <= 20)，表示不同的物品的数目。接下来的n行，每行有一个1到40之间的正整数，分别给出a1，a2……an的值。

**输出描述**：

输出不同的选择物品的方式的数目。

思路：DFS

~~~c++
#include <iostream>
#include <algorithm>
using namespace std;

const int MAXN = 21;
int weight[MAXN];
int n, res;

void DFS(int w, int index) {
    for (int i = index; i < n; i++) {
        int cal = w + weight[i];
        if (cal > 40)
            continue;
        else if (cal < 40)
            DFS(cal, i+1);
        else
            res++;
    }
}

int main() {
    while (cin >> n) {
        int total = 0;
        res = 0;
        for (int i = 0; i < n; i++) {
            cin >> weight[i];
            total += weight[i];
        }
        if (total < 40) {
            cout << 0 << endl;
            continue;
        }
        sort(weight, weight+n);
        if (weight[0] > 40) {
            cout << 0 << endl;
            continue;
        }
        DFS(0, 0);
        cout << res << endl;
    }
}
~~~

## 八皇后

[八皇后_牛客题霸_牛客网 (nowcoder.com)](https://www.nowcoder.com/practice/fbf428ecb0574236a2a0295e1fa854cb?tpId=61&tqId=29558&tPage=3&ru=/kaoyan/retest/1002&qru=/ta/pku-kaoyan/question-ranking)

**描述**

会下国际象棋的人都很清楚：皇后可以在横、竖、斜线上不限步数地吃掉其他棋子。如何将8个皇后放在棋盘上（有8 * 8个方格），使它们谁也不能被吃掉！这就是著名的八皇后问题。 对于某个满足要求的8皇后的摆放方法，定义一个皇后串a与之对应，即a=b1b2...b8，其中bi为相应摆法中第i行皇后所处的列数。已经知道8皇后问题一共有92组解（即92个不同的皇后串）。 给出一个数b，要求输出第b个串。串的比较是这样的：皇后串x置于皇后串y之前，当且仅当将x视为整数时比y小。

**输入描述**：

每组测试数据占1行，包括一个正整数b(1 <= b <= 92)

**输出描述**：

输出有n行，每行输出对应一个输入。输出应是一个正整数，是对应于b的皇后串。

### 法1：

思路：这道题花了我很长时间去做，写好代码后一直报栈溢出的错误，debug了快一个小时才发现queen==7那个条件没有return，一直在DFS遍历

具体解题方法：

1. 首先以第一个queen 1-8 for循环，每次重置use二维布尔数组为false
2. DFS传入三元组(col_num, queen, queen_s)，col_num表示当前queen的列数，queen表示第几行queen，queen_s表示已经排好的queen串
3. 每次进入DFS后，使用for循环根据col_num和queen值，设置该列和所在对角线的所有use布尔值为true，表示会被其他queen吃掉
4. 如果遇到一个位置不是true，则queen_s+当前数，并进入下一个DFS，需要注意使用tmp_use和new_queen_s来缓存，这样如果进入DFS没有找到结果，返回后还可以恢复原来的状态

~~~c++
#include <cstring>
#include <iostream>
using namespace std;

string s[92];
bool use[8][8];
int num = 0;

void DFS(int col_num, int queen, string queen_s) {
    if (queen == 7) {
        s[num] = queen_s;
        num++;
        return;
    }
    for (int i = 1; i + queen < 8; i++) {
        use[i+queen][col_num] = true;
        if (col_num+i < 8)
            use[i+queen][col_num+i] = true;
        if (col_num-i >= 0)
            use[i+queen][col_num-i] = true;
    }
    for (int i = 0; i < 8; i++) {
        bool tmp_use[8][8];
        memcpy(tmp_use, use, sizeof(use));
        string new_queen_s = queen_s;
        if (use[queen+1][i])
            continue;
        else {
            new_queen_s.push_back('0'+i+1);
            DFS(i, queen+1, new_queen_s);
            memcpy(use, tmp_use, sizeof(tmp_use));
        }
    }
}

int main() {
    for (int i = 0; i < 8; i++) {
        memset(use, false, sizeof(use));
        string queen_s = "";
        queen_s.push_back('0' + i + 1);
        DFS(i, 0, queen_s);
    }
    int b;
    while (cin >> b) {
        cout << s[b-1] << endl;
    }
    return 0;
}
~~~

### 法2：别人的DFS，更简单

~~~C++
/* DFS
 * 行从0到7逐层增加，不会存在重复放到同一行的情况
 * 列需要用bool col[8]记录某行是否已经放置
 * 对角线则需要用一个bool matrix[8][8](代码里用到矩阵名是djx)，并放到Judge(int x,int y)中判断
 * 然后思路就比较简单了，按照DFS对可扩展的状态进行递归
 * 每层的可扩展状态满足：
 *    （1）列上没有其它棋子
 *    （2）对角线上没有棋子
 * 好像把DFS中的now换成row更容易理解？
 */
#include <cstdio>
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

const int maxN = 8;
bool djx[maxN][maxN] = {false};
bool col[maxN] = {false};

vector<int> vi;        //可以用string

bool Judge(int x,int y){    //用于判断当前条件下（djx数组目前的状态下）对角线上是否已经有棋子了
    int y2 = y;
    for(int i=x;i>=0;i--){
        if(y>=0 && djx[i][y--]==true)
            return false;
        if(y2<8 && djx[i][y2++]==true)
            return false;
    }
    return true;
}
void DFS(int now,int ans){
    if(now==8){
        vi.push_back(ans);
        return ;
    }
    for(int j=0;j<8;j++){        //完全的DFS思路
        if(!col[j] && Judge(now,j)){
            col[j] = true;
            djx[now][j] = true;           //注意：题目里的所有数字都是从1开始计数，所以使用j+1记录answer
            DFS(now+1,ans*10+j+1);        //可以用string，由于最长8为十进制数，所以用int了
            col[j] = false;
            djx[now][j] = false;
        }
    }
}
int main(){
    DFS(0,0);
    sort(vi.begin(),vi.end());      //对answer进行排序
    int index;
    while(cin>>index){
        cout<<vi[index-1]<<endl;    //注意题目中所有数字均为从1计数
    }
    return 0;
}
~~~

最后修改：2023 年 06 月 18 日

如果觉得我的文章对你有用，请随意赞赏

发表评论取消回复

评论 *

私密评论

名称 *

🎲

邮箱 *

地址

Reverse（十一）
浏览次数: 2629
Win11新机鼓捣记录
浏览次数: 2382
栈~数制转换
浏览次数: 1604
C++学习
浏览次数: 1603
Python实现文件管理系统（重命名和删除）
浏览次数: 1575

顶点软件
你写得非常清晰明了，让我很容易理解你的观点。
mars
博主你好，请问怎么知道的alloc函数属于Buffer下的方法...
lj
该评论仅登录用户及评论双方可见
Mr.Guan
:@(赞一个)
Typecho
欢迎加入 Typecho 大家族

操作系统特征
浏览次数: 515
数据库学习（一）
浏览次数: 496
Reverse（三）
浏览次数: 523
数据结构与算法~查找
浏览次数: 588
链路层（一）
浏览次数: 413

机试day9

Xherlock • 2023 年 06 月 18 日

# 机试day9

## 鸡兔同笼

**描述**

**输入描述**：

每组测试数据占1行，每行一个正整数a (a < 32768)

**输出描述**：

思路：最少时要么全是兔子要么1只鸡剩下全是兔子；最多时全是鸡。出现奇数说明不满足

~~~c++
#include <iostream>
using namespace std;

## 代理服务器

**描述**

**输入描述**：

**输出描述**：

~~~
输入：
3
166.111.4.100
162.105.131.113
202.112.128.69
6
72.14.235.104
166.111.4.100
207.46.19.190
202.112.128.69
162.105.131.113
118.214.226.52
输出：
1
~~~

思路：这题真的好烧脑啊啊啊啊啊啊，但我做出来了啊啊啊啊啊啊

~~~c++
#include <cstring>
#include <iostream>
using namespace std;

memset要善用，虽然容易写错（溢出之类的？），但是不需要循环初始化值，很方便

看了下其他人的解题思路，发现有用二分法（先sort代理服务器IP）加快匹配的，也行，不过既然能pass了，那就没必要再多此一举了

## To Fill or Not to Fill

**描述**

**输入描述**：

**输出描述**：

思路：本人除了会写结构体、排序、写输入输出，对于算法设计完全是懵逼的，看了其他人思路只能自叹不如

~~~c++
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;

struct GasStation {
    double price;
    int distance;
};

bool stationCompare(GasStation x, GasStation y) {
    return x.price < y.price;
}

## n的阶乘

使用递归实现

~~~c++
#include <iostream>
using namespace std;

long long Factorial(int n) {
    if (n == 0)
        return 1;
    else
        return n * Factorial(n-1);
}

int main() {
    int n;
    while (cin >> n) {
        cout << Factorial(n) << endl;
    }
}
~~~

### 杨辉三角形

打印某一行

![format,f_auto.jpeg](http://xherlock.top/usr/uploads/2023/06/4009197352.jpeg)

~~~c++
#include <iostream>
using namespace std;

int Yanghui(int n, int i) {
    if (i == 0 || n == i + 1)
        return 1;
    else
        return Yanghui(n-1, i-1) + Yanghui(n-1, i);
}

int main() {
    int n;
    while (cin >> n) {
        for (int i = 0; i < n; i++) {
            cout << Yanghui(n, i);
            if (i != n -1)
                cout << " ";
        }
    }
}
~~~

### 全排列

**描述**

**输入描述**：

输入只有一行，是一个由不同的小写字母组成的字符串，已知字符串的长度在1到6之间。

**输出描述**：

思路：最简单的直接STL（标准库）里algorithm的next_permutation

正常思路：递归

~~~c++
#include <iostream>
#include <algorithm>
using namespace std;
string str;

void swap(int x, int y) {
    char tmp = str[x];
    str[x] = str[y];
    str[y] = tmp;
}

int main() {
    while (cin >> str) {
        sort(str.begin(), str.end());
        func(0, str.size()-1);
    }
}
~~~

### Fibonacci

求第n个Fibonacci数，思路就是递归（分而治之）

~~~c++
#include <iostream>
using namespace std;

int Fibonacci(int n) {
    if (n == 0)
        return 0;
    else if (n == 1)
        return 1;
    else
        return Fibonacci(n-1) + Fibonacci(n-2);
}

int main() {
    int n;
    while (cin >> n) {
        cout << Fibonacci(n) << endl;
    }
}
~~~

### 二叉树

**描述**

![39_1429598902788_btree.jpg](http://xherlock.top/usr/uploads/2023/06/2564805606.jpg)

**输入描述**：

输入数据包括多行，每行给出一组测试数据，包括两个整数m，n (1 <= m <= n <= 1000000000)。

**输出描述**：

对于每一组测试数据，输出一行，该行包含一个整数，给出结点m所在子树中包括的结点的数目。

~~~
输入：
3 12
0 0
输出：
4
~~~

思路：分别求左子树和右子树节点个数【分治法】

~~~c++
#include <iostream>
using namespace std;

int get_children(int m, int n) {
    if (m <= n)
        return 1 + get_children(2 * m, n) + get_children(2 * m + 1, n);
    else
        return 0;
}

int main() {
    int m, n;
    while (cin >> m >> n) {
        if (m == 0)
            break;
        cout << get_children(m, n) << endl;
    }
}
~~~

## 2的幂次方

**描述**

**输入描述**：

For each case, the input file contains a positive integer n (n<=20000).

**输出描述**：

For each case, you should output the exponential form of n an a single line.Note that,there should not be any additional white spaces in the line.

思路：需要先用while循环不断除2求出指数，在递归求指数的2次幂表示；其中如果指数为0或1的，直接s拼接即可

~~~c++
#include <iostream>
#include <vector>
using namespace std;

int main() {
    int n;
    while (cin >> n) {
        cout << func(n) << endl;
    }
}
~~~

## Catch That Cow

题目大意：给定农夫位置N，奶牛K，农夫可以行走：1min从X到X-1或X+1；传送：1min从X到2X，问需要最少时间抓到奶牛

~~~c++
#include <iostream>
#include <cstring>
#include <cstdio>
#include <queue>

using namespace std;

const int MAXN = 100001;

struct Status {
    int n, t;
    Status(int n, int t): n(n), t(t) {}
};

## Find The Multiple

给出一个正整数n，找到n的倍数m，使得m的十进制只包含0和1两种数字

思路：BFS找，此处不用担心被访问过的，因为数字始终增大，每次找10\*i、10\*i+1，这样保证了所有数均含0、1

~~~c++
#include <iostream>
#include <cstring>
#include <queue>

using namespace std;

int main() {
    int n;
    while (cin >> n) {
        if (n == 0)
            break;
        cout << BFS_search(n) << endl;
    }
    return 0;
}
~~~

小结：

* BFS：搜索求解最优解问题
* DFS：查找问题是否有解

### A Knight's Journey

![IMG_20230617_201320.jpg](http://xherlock.top/usr/uploads/2023/06/1340343705.jpg)

思路：使用DFS从A1开始遍历，需要使用递归

这里需要理解题意：pxq，行是字母，列是数字，如上图我写了个简单的格式。对于字典序，字母小的先访问，然后数字小的先访问

~~~c++
#include <iostream>
#include <cstdio>
#include <string>
#include <cstring>

using namespace std;

const int MAXN = 30;
int p, q;
bool visit[MAXN][MAXN];
int direction[8][2] = {
    {-1, -2}, {1, -2}, {-2, -1}, {2, -1}, {-2, 1}, {2, 1}, {-1, 2}, {1, 2}
};

## Square

题目：木棍拼正方形

~~~
输入：
3
4 1 1 1 1 
5 10 20 30 40 50
8 1 7 2 6 3 5 4 4
输出：
yes
no
yes
~~~

思路：三元组(sum, number, position)，sum表示当前拼凑的木棍总长，number表示已经拼凑成边长的数量，position表示当前木棍的编号

首先要按照从大到小排序木棍长度，一个边一个边的拼凑

~~~c++
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>

using namespace std;

const int MAXN = 25;
int side;
int m;
int sticks[MAXN];
bool visit[MAXN];

bool Compare(int x, int y) {
    return x > y;
}

## 神奇的口袋

**描述**

**输入描述**：

输入的第一行是正整数n (1 <= n <= 20)，表示不同的物品的数目。接下来的n行，每行有一个1到40之间的正整数，分别给出a1，a2……an的值。

**输出描述**：

输出不同的选择物品的方式的数目。

思路：DFS

~~~c++
#include <iostream>
#include <algorithm>
using namespace std;

const int MAXN = 21;
int weight[MAXN];
int n, res;

## 八皇后

**描述**

**输入描述**：

每组测试数据占1行，包括一个正整数b(1 <= b <= 92)

**输出描述**：

输出有n行，每行输出对应一个输入。输出应是一个正整数，是对应于b的皇后串。

### 法1：

思路：这道题花了我很长时间去做，写好代码后一直报栈溢出的错误，debug了快一个小时才发现queen==7那个条件没有return，一直在DFS遍历

具体解题方法：

~~~c++
#include <cstring>
#include <iostream>
using namespace std;

string s[92];
bool use[8][8];
int num = 0;

### 法2：别人的DFS，更简单

const int maxN = 8;
bool djx[maxN][maxN] = {false};
bool col[maxN] = {false};

vector<int> vi;        //可以用string

发表评论 取消回复

机试day9

发表评论取消回复