公钥密码体制
概述
对称密码体制缺点：
- 密钥管理困难（用户数量越多，所需密钥数量急剧增大）
- 系统开放性问题（必须各方信任）
- 难以提供数字签名功能（无法抗抵赖）
公钥密码体制又称非对称密码体制或双密钥密码体制，1976年由Diffie和Hellman提出，属于非对称密钥体制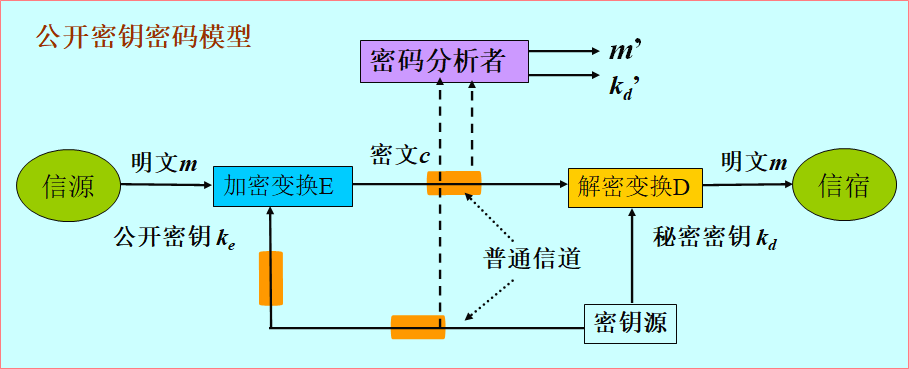
公钥密码基本思想
对公钥密码要求
- 生成密钥对计算容易
- 发送方使用接收方公钥生成密文在计算上容易
- 接收方使用自己的私钥解密密文在计算上容易
- 由公钥计算私钥在计算上不可行
- 由公钥和密文还原明文在计算上不可行
单向陷门函数
- 给出f的定义域中的任何元素x，f(x)的计算是容易的
- 给出y=f(x)中的y要计算x时，若知道设计函数f时结合进去的某种信息（陷门）则容易计算；若不知道该信息，则难以计算
目前基于一下设计单向函数和公钥密码体制：
- 大整数分解问题（RSA）
- 有限域上离散对数问题（ElGamal）
- 椭圆曲线上的离散对数问题（ECC）
公钥密码的应用
- 机密性的实现：加解密消息
- 数字签名
- 密钥分发和协商：实现在公开信道上的大规模密钥分发和协商
和对称密码体制对比
RSA公钥密码体制
数学基础：初等数论中的欧拉定理
安全性基础：大整数因子分解的困难性
RSA算法
生成密钥：
- 选择两个大素数p、q（pq互素，需保密）
- 计算$n=p\times q,\phi(n)=(p-1)\times(q-1)$
- 选择整数e使得$(\phi(n),e)=1,1<e<\phi(n)$
- 计算d，使得$d=e^{-1}mod\phi(n)$，得到公钥(e,n)，私钥d
- 加密：密文$c=m^e(mod\,n)$
- 解密：对密文，$m=c^d(mod\,n)$
RSA基本性质
- 加密解密运算具有可交换性
- 加解密算法的有效性
- 在计算上由公开的加密密钥不能求出解密密钥：当合数n足够大时，因子分解很困难
RSA的实现
快速求模n指数运算
法一：平方-乘法算法
法二：中国剩余定理（CRT）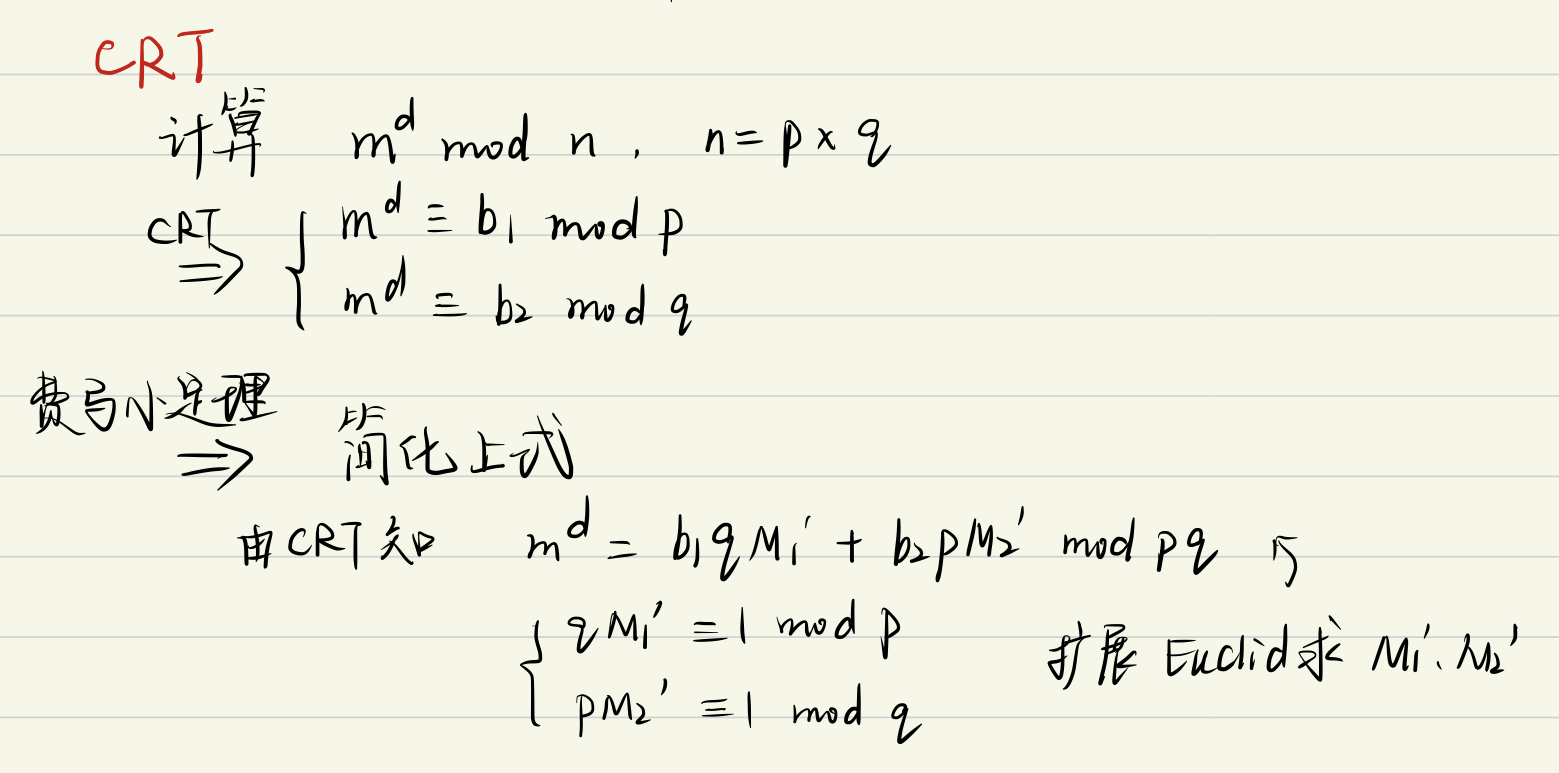
素数检测
Miller-Rabin素数概率检测法
二次探测定理：若p是一个奇素数，则方程$x^{2}=1\ mod\ p$的解只有x≡1或x≡-1
费马小定理：若不满足则p一定是合数
Wilson定理：$(p-1)!\equiv-1\ mod\ p$
RSA的安全性
基于分解大整数的困难性
现有的攻击手段：
- 对RSA的选择密文攻击
- 小加密指数e攻击
选取参数建议：
- p、q长度差不多
- p-1和q-1都应该包含大的素因子
- gcd(p-1,q-1)应该很小
- $d<n^{\frac{1}{4}}$
RSA应用中的问题
- 用户之间不要共享模数n（存在公共模数攻击）
- 不同的用户选用的素数不能相同
- 一般不能直接应用RSA进行加解密
ElGamal公钥密码体制
算法描述：
选取参数
选取大素数p，α是p的一个本原元
加密：
- 用户A先把明文M编码为一个在0到p-1之间的整数m作为传输的明文
- 用户A挑选一个秘密随机数k（2≤k≤p-2）
并计算：$c1=\alpha^k(mod\ p)$ 和 $c2=my_{B}^{k}(mod\ p)$（$y_{B}$为用户B的公开密钥）
- 用户A把二元组(c1,c2)作为密文传送给B
解密：
$m=c2(c1^{X_{B}})^{-1}$，$x_{B}$是用户B的秘密密钥
解密验证：$c2(c1^{X_{B}})^{-1}mod\ p=my^{k}(\alpha^{kx})^{-1}mod\ p=m\alpha^{kx}(\alpha^{kx})^{-1}mod\ p=m$
算法特点：
- 非确定性
- 密文空间大于明文空间
算法安全性：
- 安全性基于计算Zp上离散对数的困难性
- 要使用不同的随机数k来加密不同的信息
- 随机数k不可预测
椭圆曲线密码体制（ECC）
安全性基于椭圆曲线离散对数问题的难解性，同有限域上的离散对数相比
- 密钥长度小
- 算法性能好
椭圆曲线
由二元三次方程定义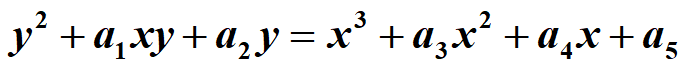
不同数域上的椭圆曲线的表示和运算是不同的
引入无穷远点O，使椭圆曲线上解点的集合构成一个交换群，定义如下加法规则：
- O称为加法单位元，对ECC上任意点有：P+O=P
- 对点P(x,y)，有点Q(x,-y)满足：P+Q=O，称Q为P的逆元，记为-P
- 对不互逆的点P(x1,y1)，Q(x2,y2)
nP=O，n为最小正整数，则称n为点P的阶
椭圆曲线密码体制算法
- 密码系统参数的生成
选取有限域GF(q)，和定义在GF(q)上的一条椭圆曲线E(a,b)，和E(a,b)上一个阶为大素数n的点G（基点）——三者为公开参数
- 密钥生成：在[2,n-1]中随机选取一个整数dA，计算PA=dA*G（公钥PA，私钥dA）
加密：
- 通过某种方式将明文消息m通过编码映射到E上的点Pm
- 在区间[2,n-1]中随机选取一个整数k
- 计算c1=kG，c2=Pm+kPA，传送Cm=(c1.c2)
- 解密：Pm=c2-dA*c1
攻击难点在于Q=kP，给定k、P容易计算Q，给定P、Q难以解出k
Menezes-Vanstone公钥密码体制
是在椭圆曲线上的一个有效实现，解决椭圆曲线明文必须编码映射到椭圆曲线上的点
用户B将源消息m变化成基域GF(p)上的二元组(m1,m2)，并执行加密算法：
- 在区间[2,n-1]中随机选取一个整数k
- 计算(c1,c2,c3)，c1=kG，Y=(y1,y2)=kPA，c2=y1m1(mod p)，c3=y2m2(mod p)
PA=dAG为用户A的公开密钥
A收到密文后解密
- Z=(z1,z2)=dAc1
- 计算明文m=(m1,m2)=$(c_{2}z1^{-1}(mod\ p),c_{3}z2^{-1}(mod\ p))$
