机试day10

博主： Xherlock
发布时间：2023 年 06 月 25 日
348 次浏览
暂无评论
2137字数
分类： C/C++&机试

# 机试day10

## 畅通工程

[畅通工程_牛客题霸_牛客网 (nowcoder.com)](https://www.nowcoder.com/practice/4878e6c6a24e443aac5211d194cf3913?tpId=63&tqId=29573&tPage=1&ru=%2Fkaoyan%2Fretest%2F9001&qru=%2Fta%2Fzju-kaoyan%2Fquestion-ranking)

**描述**

某省调查城镇交通状况，得到现有城镇道路统计表，表中列出了每条道路直接连通的城镇。省政府“畅通工程”的目标是使全省任何两个城镇间都可以实现交通（但不一定有直接的道路相连，只要互相间接通过道路可达即可）。问最少还需要建设多少条道路？

**输入描述**：

测试输入包含若干测试用例。每个测试用例的第1行给出两个正整数，分别是城镇数目N ( < 1000 )和道路数目M；随后的M行对应M条道路，每行给出一对正整数，分别是该条道路直接连通的两个城镇的编号。为简单起见，城镇从1到N编号。   注意:两个城市之间可以有多条道路相通,也就是说   3 3   1 2   1 2   2 1   这种输入也是合法的   当N为0时，输入结束，该用例不被处理。

**输出描述**：

对每个测试用例，在1行里输出最少还需要建设的道路数目。

~~~
输入：
4 2
1 3
4 3
3 3
1 2
1 3
2 3
5 2
1 2
3 5
999 0
0
输出：
1
0
2
998
~~~

### 法1：计算集合数目

思路：初始每个城镇都是孤立的，读入建成的道路，将道路连接的城镇所在集合合并，表示两个集合中的结点都已连通。最后只需计算有多少集合即可

~~~c++
#include <iostream>
using namespace std;

const int MAXN = 1000;
int father[MAXN];   // 父亲结点
int height[MAXN];   // 结点高度

void Initial(int n) {                   // 初始化
    for (int i = 0; i <= n; i++) {
        father[i] = i;                  // 每个结点的父亲为自己
        height[i] = 0;                  // 每个结点的高度为0
    }
}

int Find(int x) {       // 查找根结点
    if (x != father[x]) {	// 如果相等，说明此时是父结点
        father[x] = Find(father[x]);	// 否则继续找父结点的父结点
    }
    return father[x];
}

void Union(int x, int y) {	// 合并集合
    x = Find(x);	// 首先找到集合的根结点
    y = Find(y);
    if (x != y) {	// 若根结点不同，说明是两个集合，需要进行合并，合并原理是尽可能使树高增加较少
        if (height[x] < height[y]) {
            father[x] = y;	// 高度低的集合树根结点的父结点指向另一个集合的根结点
        } else if (height[x] > height[y]) {
            father[y] = x;
        } else {
            father[y] = x;	// 若高度相等把y加到x的子结点，同时x的高度+1
            height[x]++;
        }
    }
}

int main() {
    int n, m;
    while (cin >> n) {
        if (n == 0)
            break;
        cin >> m;
        Initial(n);
        while (m--) {
            int x, y;
            cin >> x >> y;
            Union(x, y);
        }
        int answer = -1;
        for (int i = 1; i <= n; i++) {
            if (Find(i) == i) {	// 如果不相等，说明此结点不是集合的根结点，反之是根结点，集合数+1（答案）
                answer++;
            }
        }
        cout << answer << endl;
    }
    return 0;
}
~~~

注！！！记住此模板，可以用到很多图论题目中

### 法2：更简单的法使用向量

~~~c++
#include<iostream>
#include<vector>
using namespace std;

int main(){
    int n, m;
    while(cin >> n >> m){
        int t = n;
        vector<int> v(n + 1,-1);
        while(m--){
            int x,y;
            cin>>x>>y;
            int a = x, b = y;
            while (v[a] != -1)	//一直找到集合的根结点
                a = v[a];
            while (v[b] != -1)
                b = v[b];
            if(a==b)			// 根结点相同
                continue;
            else 
                v[b] = x, t -= 1;	//合并集合
        }
        v.clear();
        cout<<t-1<<endl;
    }
}
~~~

## 连通图

[连通图_牛客题霸_牛客网 (nowcoder.com)](https://www.nowcoder.com/practice/569e89823a5141fe8a11ab7d4da21edf?tpId=65&tqId=29622&tPage=1&ru=/kaoyan/retest/4001&qru=/ta/jlu-kaoyan/question-ranking)

**描述**

给定一个无向图和其中的所有边，判断这个图是否所有顶点都是连通的。

**输入描述**：

每组数据的第一行是两个整数 n 和 m（0<=n<=1000）。n 表示图的顶点数目，m 表示图中边的数目。随后有 m 行数据，每行有两个值 x 和 y（0<x, y <=n），表示顶点 x 和 y 相连，顶点的编号从 1 开始计算。输入不保证这些边是否重复。

**输出描述**：

对于每组输入数据，如果所有顶点都是连通的，输出"YES"，否则输出"NO"。

思路：直接套用上一题的模板即可，最后集合数大于0，说明图没有连通

~~~c++
#include <iostream>
using namespace std;

const int MAXN = 1000;
int father[MAXN];   // 父亲结点
int height[MAXN];   // 结点高度

int Find(int x) {       // 查找根结点
    if (x != father[x]) {
        father[x] = Find(father[x]);
    }
    return father[x];
}

void Union(int x, int y) {
    x = Find(x);
    y = Find(y);
    if (x != y) {
        if (height[x] < height[y]) {
            father[x] = y;
        } else if (height[x] > height[y]) {
            father[y] = x;
        } else {
            father[y] = x;
            height[x]++;
        }
    }
}

int main() {
    int n, m;
    while (cin >> n) {
        if (n == 0)
            break;
        cin >> m;
        Initial(n);
        while (m--) {
            int x, y;
            cin >> x >> y;
            Union(x, y);
        }
        int answer = -1;
        for (int i = 1; i <= n; i++) {
            if (Find(i) == i) {
                answer++;
            }
        }
        if (answer == 0)
            cout << "YES" << endl;
        else
            cout << "NO" << endl;
    }
    return 0;
}
~~~

## Is It A Tree?

[Is It A Tree?_牛客题霸_牛客网 (nowcoder.com)](https://www.nowcoder.com/practice/1c5fd2e69e534cdcaba17083a5c56335?tpId=61&tqId=29506&tPage=1&ru=/kaoyan/retest/1002&qru=/ta/pku-kaoyan/question-ranking)

**描述**

A tree is a well-known data structure that is either empty (null, void, nothing) or is a set of one or more nodes connected by directed edges between nodes satisfying the following properties. There is exactly one node, called the root, to which no directed edges point. Every node except the root has exactly one edge pointing to it. There is a unique sequence of directed edges from the root to each node. For example, consider the illustrations below, in which nodes are represented by circles and edges are represented by lines with arrowheads. The first two of these are trees, but the last is not.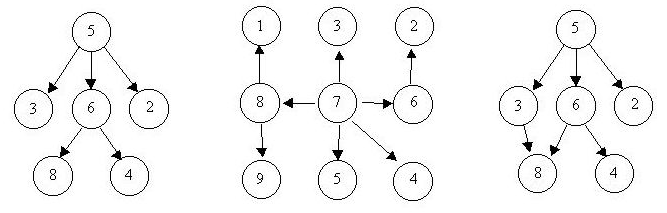

![39_1429713497666_1481.png](http://xherlock.top/usr/uploads/2023/06/2178570252.png)

In this problem you will be given several descriptions of collections of nodes connected by directed edges. For each of these you are to determine if the collection satisfies the definition of a tree or not.

**输入描述**：

The input will consist of a sequence of descriptions (test cases) followed by a pair of negative integers. Each test case will consist of a sequence of edge descriptions followed by a pair of zeroes Each edge description will consist of a pair of integers; the first integer identifies the node from which the edge begins, and the second integer identifies the node to which the edge is directed. Node numbers will always be greater than zero and less than 10000.

**输出描述**：

For each test case display the line "Case k is a tree." or the line "Case k is not a tree.", where k corresponds to the test case number (they are sequentially numbered starting with 1).

~~~
输入：
6 8  5 3  5 2  6 4
5 6  0 0

8 1  7 3  6 2  8 9  7 5
7 4  7 8  7 6  0 0

3 8  6 8  6 4
5 3  5 6  5 2  0 0
-1 -1
输出：
Case 1 is a tree.
Case 2 is a tree.
Case 3 is not a tree.
~~~

思路：仍然使用图来解决，但需要使用有向图，设置入度

~~~c++
#include <iostream>
using namespace std;

const int MAXN = 10000;
int father[MAXN];
int height[MAXN];
int inDegree[MAXN];
bool visit[MAXN];

void Initial() {
    for (int i = 0; i < MAXN; i++) {
        father[i] = i;
        height[i] = 0;
        inDegree[i] = 0;
        visit[i] = false;
    }
}

int Find(int x) {
    if (x != father[x])
        father[x] = Find(father[x]);
    return father[x];
}

void Union(int x, int y) {
    x = Find(x);
    y = Find(y);
    if (x != y) {
        if (height[x] < height[y])
            father[x] = y;
        else if (height[x] > height[y])
            father[y] = x;
        else {
            father[y] = x;
            height[x]++;
        }
    }
}

bool isTree() {
    bool flag = true;
    int component = 0;
    int root = 0;
    for (int i = 0; i < MAXN; i++) {
        if (!visit[i])
            continue;
        if (father[i] == i)
            component++;
        if (inDegree[i] == 0)
            root++;
        else if (inDegree[i] > 1)
            flag = false;
    }
    if (component != 1 || root != 1)
        flag = false;
    if (component == 0 && root == 0)
        flag = true;
    return flag;
}

int main() {
    int p, q;
    Initial();
    int caseNumber = 0;
    while (cin >> p >> q) {
        if (p == -1 && q == -1)
            break;
        if (p == 0 && q == 0) {
            if (isTree())
                cout << "Case " << ++caseNumber << " is a tree." << endl;
            else
                cout << "Case " << ++caseNumber << " is not a tree." << endl;
            Initial();
        } else {
            Union(p, q);
            inDegree[q]++;
            visit[p] = true;
            visit[q] = true;
        }
    }
}
~~~

## 第一题

[第一题_牛客题霸_牛客网 (nowcoder.com)](https://www.nowcoder.com/practice/7c29cdfa28274c86afc9e88c07448a10?tpId=62&tqId=31040&tPage=2&ru=/kaoyan/retest/2002&qru=/ta/sju-kaoyan/question-ranking)

**描述**

该题的目的是要你统计图的连通分支数。

**输入描述**：

每个输入文件包含若干行，每行两个整数i,j，表示节点i和j之间存在一条边。
（请使用循环输入，可以参考该网址：https://www.nowcoder.com/discuss/276）

**输出描述**：

输出每个图的联通分支数。

~~~
输入：
1 4
4 3
5 5
输出：
2
~~~

思路：并查集，检查最终集合数目即可

~~~c++
#include <iostream>
using namespace std;

const int MAXN = 1000000;
int father[MAXN];
int height[MAXN];
bool visit[MAXN];

void Initial() {
    for (int i = 0; i < MAXN; i++) {
        father[i] = i;
        height[i] = 0;
        visit[i] = false;
    }
}

int Find(int x) {
    if (x != father[x])
        father[x] = Find(father[x]);
    return father[x];      
}

int main() {
    int i, j;
    Initial();
    while (cin >> i >> j) {
        Union(i, j);
        visit[i] = true, visit[j] = true;
    }
    int answer = 0;
    for (int k = 0; k < MAXN; k++) {
        if (k == father[k] && visit[k])
            answer++;
    }
    cout << answer;
}
~~~

改进：本代码有缺陷，由于题目没有说明输入范围，因此最好使用map\<int, int\> father替换int father[MAXN]，这样就不用设置MAXN

## Head of a Gang

[Head of a Gang_牛客题霸_牛客网 (nowcoder.com)](https://www.nowcoder.com/practice/a31b1ea6c87647bc86e382acaf21c53b?tpId=63&tqId=29585&tPage=2&ru=%2Fkaoyan%2Fretest%2F9001&qru=%2Fta%2Fzju-kaoyan%2Fquestion-ranking)

**描述**

One way that the police finds the head of a gang is to check people's phone calls. If there is a phone call between A and B, we say that A and B is related. The weight of a relation is defined to be the total time length of all the phone calls made between the two persons. A "Gang" is a cluster of more than 2 persons who are related to each other with total relation weight being greater than a given threthold K. In each gang, the one with maximum total weight is the head. Now given a list of phone calls, you are supposed to find the gangs and the heads.

**输入描述**：

For each case, the first line contains two positive numbers N and K (both less than or equal to 1000), the number of phone calls and the weight threthold, respectively. Then N lines follow, each in the following format: Name1 Name2 Time where Name1 and Name2 are the names of people at the two ends of the call, and Time is the length of the call. A name is a string of **three capital letters** chosen from A-Z. A time length is a positive integer which is no more than 1000 minutes.

**输出描述**：

For each test case, first print in a line the total number of gangs. Then for each gang, print in a line the name of the head and the total number of the members. It is guaranteed that the head is unique for each gang. The output must be sorted according to the alphabetical order of the names of the heads.

**思路**：仍然是并查集，设置了一堆数据结构来处理

* 调用的函数和之前无区别，分别是初始化、找根结点、合并集合
* 新设置了两种结构体，分别是Node和Graph
  * Node的i表示name首字母-'A'的数字值，weight表示该结点的权值
  * Graph的total_w表示集合所有结点的权值和（最后会除以2，因为所有结点权值算了两次）、num表示集合中结点数
* 接下来的思路，看注释

~~~c++
#include <iostream>
#include <map>
#include <vector>
#include <cstring>
using namespace std;

const int MAXN = 1000;
int father[MAXN];
int height[MAXN];
int weight[26];

void Initial() {
    for (int i = 0; i < MAXN; i++) {
        father[i] = i;
        height[i] = 0;
    }
    memset(weight, 0, sizeof(weight));
}

int Find(int x) {
    if (x != father[x])
        father[x] = Find(father[x]);
    return father[x];      
}

struct Node {
    int i, weight;
    Node(int a, int b): i(a), weight(b) {}
};
struct Graph {
    int total_w, num;
    Graph(int a, int b): total_w(a), num(b) {}
};

int main() {
    int N, K;
    while (cin >> N >> K) {
        Initial();
        string name1, name2;
        int time, flag;
        for (int i = 0; i < N; i++) {	// 本方法缺陷在这里，虽然题目说了name由三个大写字母，但提交发现有的只有一个大写字母，甚至不确定有没有可能给的三个大写字母都不同，如果这样的话本方法失败
            cin >> name1 >> name2 >> time;
            weight[name1[0]-'A'] += time;	// 每个结点值唯一值，并增加权重值
            weight[name2[0]-'A'] += time;
            Union(name1[0]-'A', name2[0]-'A');	// 把首字母和A的数字差作为结点值构建并查集
        }
        flag = name1.size();	// 记录name长度
        map<int, int> myMap;   // 根值和集合id
        vector<Graph> graph;	// 图，存储集合所有结点权值和、结点数目
        vector<Node> G_max;		// 结点，存储所有集合权值最大的结点信息
        int g_num = 0;
        for (int i = 0; i < 26; i++) {
            if (weight[i] == 0)	// 该字母未出现
                continue;
            int root = Find(i);	// 获取该集合根结点值
            if (myMap.count(root) == 0) {  // 遇到新的集合
                myMap[root] = g_num;
                graph.push_back(Graph(weight[i], 1));   // 集合总权值加入到vector中
                G_max.push_back(Node(i, weight[i]));    // 结点加入到vector中
                g_num++;
            } else {	// 之前就遇到过，则权值和增加，结点数目+1，最大权值更新
                int j = myMap[root];
                graph[j].total_w += weight[i];            // 更新加上权值
                graph[j].num++;
                if (G_max[j].weight < weight[i])    // 更新修改为该集合的最大权值
                    G_max[j] = Node(i, weight[i]);
            }
        }
        int gang_num = 0;
        for (int i = 0; i < g_num; i++) {	// 先获取可以视为gang的集合数目并打印
            if (graph[i].total_w / 2 > K && graph[i].num> 2)
                gang_num++;
        }
        cout << gang_num << endl;
        for (int i = 0; i < g_num; i++) {
            if (graph[i].total_w / 2 > K && graph[i].num> 2) {
                string name;
                name += ('A' + G_max[i].i);	// 获取name首字母的大写字母
                for (int j = 0; j < flag; j++)
                    cout << name;	// 循环输出
                cout << " " << graph[i].num << endl;	// 打印集合结点数目
            }
        }
    }
}
~~~

改进：对于字符串可能不同可以考虑使用map映射name和id（看的他人代码）

![image-20230625105954973.png](http://xherlock.top/usr/uploads/2023/06/1549876060.png)

**知识点**

最小生成树（MST）：在一个无向连通图中，若存在一个连通子图，它包含原图中的所有顶点和部分边，且子图不存在回路，则称子图为原图的一棵生成树。在带权无向连通图中，所有生成树中边权和最小的那棵被称为最小生成树

构造方法：**Kruskal**算法和Prim算法，其中Kruskal算法更简单且效率非常高

Kruskal原理：在要求解的连通图中，任意选择一些点属于集合A，剩余属于集合B，最小生成树必定存在一条权值最小的边，并且这条边两个顶点分别属于A、B的边【反证法证明】

**算法步骤**：

1. 初始时所有顶点属于孤立的集合
2. 按照边权递增顺序遍历所有边，若遍历到的边的两个顶点分属不同的集合，则确定该边为最小生成树上的一条边，并将该边两个顶点分属的集合合并
3. 遍历完所有边后，若原图连通，则被选取的边和所有顶点构成最小生成树，若不连通则最小生成树不存在

## 还是畅通工程

[还是畅通工程_牛客题霸_牛客网 (nowcoder.com)](https://www.nowcoder.com/practice/d6bd75dbb36e410995f8673a6a2e2229?tpId=63&tqId=29595&tPage=2&ru=/kaoyan/retest/9001&qru=/ta/zju-kaoyan/question-ranking)

**描述**

某省调查乡村交通状况，得到的统计表中列出了任意两村庄间的距离。省政府“畅通工程”的目标是使全省任何两个村庄间都可以实现公路交通（但不一定有直接的公路相连，只要能间接通过公路可达即可），并要求铺设的公路总长度为最小。请计算最小的公路总长度。

**输入描述**：

测试输入包含若干测试用例。每个测试用例的第1行给出村庄数目N ( < 100 )；随后的N(N-1)/2行对应村庄间的距离，每行给出一对正整数，分别是两个村庄的编号，以及此两村庄间的距离。为简单起见，村庄从1到N编号。   当N为0时，输入结束，该用例不被处理。

**输出描述**：

对每个测试用例，在1行里输出最小的公路总长度。

思路：仍然使用并查集，只不过Union返回的是两个结点是否同为一个集合的bool值，同时定义了Edge结构接收结点值和距离，并使用sort+自定义比较函数Compare来从小到大排列，并依次遍历边

本题结果必定有最小生成树，因此不必检查图是否连通

~~~c++
#include <iostream>
#include <algorithm>
#include <map>
using namespace std;

const int MAXN = 100;
int father[MAXN];
int height[MAXN];

struct Edge {
    int node1, node2, dist;
};

bool Compare(Edge x, Edge y) {
    return x.dist < y.dist;
}

void Initial(int n) {
    for (int i = 0; i < n; i++) {
        father[i] = i;
        height[i] = 0;
    }
}

int Find(int x) {
    if (x != father[x])
        father[x] = Find(father[x]);
    return father[x];
}

bool Union(int x, int y) {
    x = Find(x);
    y = Find(y);
    if (x != y) {
        if (height[x] < height[y])
            father[x] = y;
        else if (height[x] > height[y])
            father[y] = x;
        else {
            father[y] = x;
            height[x]++;
        }
        return true;
    } else 
        return false;
}

int main() {
    int N;
    while (cin >> N) {
        if (N == 0)
            break;
        Initial(N);
        int relation = N * (N - 1) / 2;
        Edge all[relation];
        for (int i = 0; i < relation; i++) {
            cin >> all[i].node1 >> all[i].node2 >> all[i].dist;   
        }
        sort(all, all + relation, Compare);
        int min_len = 0;
        for (int i = 0; i < relation; i++) {
            if (Union(all[i].node1-1, all[i].node2-1)) {
                min_len += all[i].dist;
            }
        }
        cout << min_len << endl;
    }
}
~~~

## 继续畅通工程

[继续畅通工程_牛客题霸_牛客网 (nowcoder.com)](https://www.nowcoder.com/practice/16212f7d46e44174b5505997ea998538?tpId=63&tqId=29565&tPage=1&ru=/kaoyan/retest/9001&qru=/ta/zju-kaoyan/question-ranking)

**描述**

省政府“畅通工程”的目标是使全省任何两个村庄间都可以实现公路交通（但不一定有直接的公路相连，只要能间接通过公路可达即可）。现得到城镇道路统计表，表中列出了任意两城镇间修建道路的费用，以及该道路是否已经修通的状态。现请你编写程序，计算出全省畅通需要的最低成本。

**输入描述**：

测试输入包含若干测试用例。每个测试用例的第1行给出村庄数目N ( 1< N < 100 )；随后的 N(N-1)/2 行对应村庄间道路的成本及修建状态，每行给4个正整数，分别是两个村庄的编号（从1编号到N），此两村庄间道路的成本，以及修建状态：1表示已建，0表示未建。   当N为0时输入结束。

**输出描述**：

每个测试用例的输出占一行，输出全省畅通需要的最低成本。

思路：在上一题基础上结构体Edge增加新的isBuild变量表示路是否修建，Compare重新编写，使得为1的排前面

**注意**：做这道题时发现测试报错，原因在Union里输入的数字应该-1，因为初始化是从0\~N-1

~~~c++
#include <iostream>
#include <algorithm>
#include <map>
using namespace std;

const int MAXN = 100;
int father[MAXN];
int height[MAXN];

struct Edge {
    int node1, node2, cost, isBuild;
};

bool Compare(Edge x, Edge y) {
    if (x.isBuild != y.isBuild)
        return x.isBuild > y.isBuild;
    else
        return x.cost < y.cost;
}

void Initial(int n) {
    for (int i = 0; i < n; i++) {
        father[i] = i;
        height[i] = 0;
    }
}

int Find(int x) {
    if (x != father[x])
        father[x] = Find(father[x]);
    return father[x];
}

int main() {
    int N;
    while (cin >> N) {
        if (N == 0)
            break;
        Initial(N);
        int relation = N * (N - 1) / 2;
        Edge all[relation];
        for (int i = 0; i < relation; i++) {
            cin >> all[i].node1 >> all[i].node2 >> all[i].cost >> all[i].isBuild;   
        }
        sort(all, all + relation, Compare);
        int min_cost = 0;
        for (int i = 0; i < relation; i++) {
            if (Union(all[i].node1-1, all[i].node2-1)) {
                if (all[i].isBuild == 0)
                    min_cost += all[i].cost;
            }
        }
        cout << min_cost << endl;
    }
}
~~~

另外一种思路是，如果遇到isBuild为1，把对应边的长度设置为0也可以

## Freckles

[Freckles_牛客题霸_牛客网 (nowcoder.com)](https://www.nowcoder.com/practice/41b14b4cd0e5448fb071743e504063cf?tpId=61&tqId=29512&tPage=1&ru=/kaoyan/retest/1002&qru=/ta/pku-kaoyan/question-ranking)

**描述**

In an episode of the Dick Van Dyke show, little Richie connects the freckles on his Dad's back to form a picture of the Liberty Bell. Alas, one of the freckles turns out to be a scar, so his Ripley's engagement falls through.   Consider Dick's back to be a plane with freckles at various (x,y) locations. Your job is to tell Richie how to connect the dots so as to minimize the amount of ink used. Richie connects the dots by drawing straight lines between pairs, possibly lifting the pen between lines. When Richie is done there must be a sequence of connected lines from any freckle to any other freckle.

**输入描述**：

The first line contains 0 < n <= 100, the number of freckles on Dick's back. For each freckle, a line follows; each following line contains two real numbers indicating the (x,y) coordinates of the freckle.

**输出描述**：

Your program prints a single real number to two decimal places: the minimum total length of ink lines that can connect all the freckles.

思路：题目大意是给出多个坐标，求出连接所有坐标的最小距离

我是把Node转为Edge来做，还是并查集，需要注意数据类型使用double

~~~c++
#include <iostream>
#include <algorithm>
#include <cmath>
#include <iomanip>
using namespace std;

const int MAXN = 100;
int father[MAXN];
int height[MAXN];

struct Edge {
    int node1, node2;
    double dist;
};

struct Node {
    double x, y;
};

bool Compare(Edge x, Edge y) {
    return x.dist < y.dist;
}

void Initial(int n) {
    for (int i = 0; i < n; i++) {
        father[i] = i;
        height[i] = 0;
    }
}

int Find(int x) {
    if (x != father[x])
        father[x] = Find(father[x]);
    return father[x];
}

int main() {
    int N;
    while (cin >> N) {
        Initial(N);
        Node nodes[N];
        for (int i = 0; i < N; i++)
            cin >> nodes[i].x >> nodes[i].y;
        int relation = N * (N - 1) / 2;
        Edge all[relation];
        int k = 0;
        // 计算边
        for (int i = 0; i < N - 1; i++) {
            for (int j = i + 1; j < N; j++) {
                all[k].node1 = i;
                all[k].node2 = j;
                all[k].dist = sqrt(pow(nodes[i].x-nodes[j].x, 2)+pow(nodes[i].y-nodes[j].y, 2));
                k++;
            }
        }
        sort(all, all + relation, Compare);
        double min_len = 0;
        for (int i = 0; i < relation; i++) {
            if (Union(all[i].node1, all[i].node2)) {
                min_len += all[i].dist;
            }
        }
        cout << fixed << setprecision(2);
        cout << min_len << endl;
    }
}
~~~

## Jungle Roads

描述

The Head Elder of the tropical island of Lagrishan has a problem. A burst of foreign aid money was spent on extra roads between villages some years ago. But the jungle overtakes roads relentlessly, so the large road network is too expensive to maintain. The Council of Elders must choose to stop maintaining some roads. The map above on the left shows all the roads in use now and the cost in aacms per month to maintain them. Of course there needs to be some way to get between all the villages on maintained roads, even if the route is not as short as before. The Chief Elder would like to tell the Council of Elders what would be the smallest amount they could spend in aacms per month to maintain roads that would connect all the villages. The villages are labeled A through I in the maps above. The map on the right shows the roads that could be maintained most cheaply, for 216 aacms per month. Your task is to write a program that will solve such problems.（ps:如果不是连通图的话，最后的结果输出不用包含不在连通图里的那些点）

**输入描述**：

The input consists of one to 100 data sets, followed by a final line containing only 0. Each data set starts with a line containing only a number n, which is the number of villages, 1 < n < 27, and the villages are labeled with the first n letters of the alphabet, capitalized. Each data set is completed with n-1 lines that start with village labels in alphabetical order. There is no line for the last village. Each line for a village starts with the village label followed by a number, k, of roads from this village to villages with labels later in the alphabet. If k is greater than 0, the line continues with data for each of the k roads. The data for each road is the village label for the other end of the road followed by the monthly maintenance cost in aacms for the road. Maintenance costs will be positive integers less than 100. All data fields in the row are separated by single blanks. The road network will always allow travel between all the villages. The network will never have more than 75 roads. No village will have more than 15 roads going to other villages (before or after in the alphabet). In the sample input below, the first data set goes with the map above.

**输出描述**：

The output is one integer per line for each data set: the minimum cost in aacms per month to maintain a road system that connect all the villages. Caution: A brute force solution that examines every possible set of roads will not finish within the one minute time limit.

思路：题目大意就是给了一堆边，让你找最小连通图

做法完全和前面相同，无非是换了数据结构来存储数据，本方法使用了vector来存储边

~~~c++
#include <iostream>
#include <algorithm>
#include <map>
#include <vector>
using namespace std;

const int MAXN = 26;
int father[MAXN];
int height[MAXN];

struct Edge {
    int node1, node2, dist;
    Edge(int a, int b, int c): node1(a), node2(b), dist(c) {}
};

bool Compare(Edge x, Edge y) {
    return x.dist < y.dist;
}

void Initial(int n) {
    for (int i = 0; i < n; i++) {
        father[i] = i;
        height[i] = 0;
    }
}

int Find(int x) {
    if (x != father[x])
        father[x] = Find(father[x]);
    return father[x];
}

int main() {
    int n;
    while (cin >> n) {
        if (n == 0)
            break;
        Initial(n);
        vector<Edge> e;
        for (int i = 0; i < n-1; i++) {
            char start;
            int k;
            cin >> start >> k;
            for (int j = 0; j < k; j++) {
                char village;
                int dist;
                cin >> village >> dist;
                e.push_back(Edge(start-'A', village-'A', dist));
            }
        }
        sort(e.begin(), e.end(), Compare);
        int min_len = 0;
        for (int i = 0; i < e.size(); i++) {
            if (Union(e[i].node1, e[i].node2)) {
                min_len += e[i].dist;
            }
        }
        cout << min_len << endl;
    }
}
~~~

最后修改：2023 年 06 月 25 日

如果觉得我的文章对你有用，请随意赞赏

发表评论取消回复

评论 *

私密评论

名称 *

🎲

邮箱 *

地址

Reverse（十一）
浏览次数: 2629
Win11新机鼓捣记录
浏览次数: 2382
栈~数制转换
浏览次数: 1604
C++学习
浏览次数: 1603
Python实现文件管理系统（重命名和删除）
浏览次数: 1575

顶点软件
你写得非常清晰明了，让我很容易理解你的观点。
mars
博主你好，请问怎么知道的alloc函数属于Buffer下的方法...
lj
该评论仅登录用户及评论双方可见
Mr.Guan
:@(赞一个)
Typecho
欢迎加入 Typecho 大家族

I/O管理和磁盘调度
浏览次数: 487
并发性：互斥和同步
浏览次数: 751
Sqli-labs学习3
浏览次数: 696
第一个程序
浏览次数: 817
关系模型
浏览次数: 605

机试day10

Xherlock • 2023 年 06 月 25 日

# 机试day10

## 畅通工程

**描述**

**输入描述**：

**输出描述**：

对每个测试用例，在1行里输出最少还需要建设的道路数目。

~~~
输入：
4 2
1 3
4 3
3 3
1 2
1 3
2 3
5 2
1 2
3 5
999 0
0
输出：
1
0
2
998
~~~

### 法1：计算集合数目

思路：初始每个城镇都是孤立的，读入建成的道路，将道路连接的城镇所在集合合并，表示两个集合中的结点都已连通。最后只需计算有多少集合即可

~~~c++
#include <iostream>
using namespace std;

const int MAXN = 1000;
int father[MAXN];   // 父亲结点
int height[MAXN];   // 结点高度

注！！！记住此模板，可以用到很多图论题目中

### 法2：更简单的法使用向量

~~~c++
#include<iostream>
#include<vector>
using namespace std;

## 连通图

**描述**

给定一个无向图和其中的所有边，判断这个图是否所有顶点都是连通的。

**输入描述**：

**输出描述**：

对于每组输入数据，如果所有顶点都是连通的，输出"YES"，否则输出"NO"。

思路：直接套用上一题的模板即可，最后集合数大于0，说明图没有连通

~~~c++
#include <iostream>
using namespace std;

const int MAXN = 1000;
int father[MAXN];   // 父亲结点
int height[MAXN];   // 结点高度

int Find(int x) {       // 查找根结点
    if (x != father[x]) {
        father[x] = Find(father[x]);
    }
    return father[x];
}

int main() {
    int n, m;
    while (cin >> n) {
        if (n == 0)
            break;
        cin >> m;
        Initial(n);
        while (m--) {
            int x, y;
            cin >> x >> y;
            Union(x, y);
        }
        int answer = -1;
        for (int i = 1; i <= n; i++) {
            if (Find(i) == i) {
                answer++;
            }
        }
        if (answer == 0)
            cout << "YES" << endl;
        else
            cout << "NO" << endl;
    }
    return 0;
}
~~~

## Is It A Tree?

**描述**

![39_1429713497666_1481.png](http://xherlock.top/usr/uploads/2023/06/2178570252.png)

**输入描述**：

**输出描述**：

For each test case display the line "Case k is a tree." or the line "Case k is not a tree.", where k corresponds to the test case number (they are sequentially numbered starting with 1).

~~~
输入：
6 8  5 3  5 2  6 4
5 6  0 0

8 1  7 3  6 2  8 9  7 5
7 4  7 8  7 6  0 0

3 8  6 8  6 4
5 3  5 6  5 2  0 0
-1 -1
输出：
Case 1 is a tree.
Case 2 is a tree.
Case 3 is not a tree.
~~~

思路：仍然使用图来解决，但需要使用有向图，设置入度

~~~c++
#include <iostream>
using namespace std;

const int MAXN = 10000;
int father[MAXN];
int height[MAXN];
int inDegree[MAXN];
bool visit[MAXN];

void Initial() {
    for (int i = 0; i < MAXN; i++) {
        father[i] = i;
        height[i] = 0;
        inDegree[i] = 0;
        visit[i] = false;
    }
}

int Find(int x) {
    if (x != father[x])
        father[x] = Find(father[x]);
    return father[x];
}

## 第一题

**描述**

该题的目的是要你统计图的连通分支数。

**输入描述**：

每个输入文件包含若干行，每行两个整数i,j，表示节点i和j之间存在一条边。
（请使用循环输入，可以参考该网址：https://www.nowcoder.com/discuss/276）

**输出描述**：

输出每个图的联通分支数。

~~~
输入：
1 4
4 3
5 5
输出：
2
~~~

思路：并查集，检查最终集合数目即可

~~~c++
#include <iostream>
using namespace std;

const int MAXN = 1000000;
int father[MAXN];
int height[MAXN];
bool visit[MAXN];

void Initial() {
    for (int i = 0; i < MAXN; i++) {
        father[i] = i;
        height[i] = 0;
        visit[i] = false;
    }
}

int Find(int x) {
    if (x != father[x])
        father[x] = Find(father[x]);
    return father[x];      
}

改进：本代码有缺陷，由于题目没有说明输入范围，因此最好使用map\<int, int\> father替换int father[MAXN]，这样就不用设置MAXN

## Head of a Gang

**描述**

**输入描述**：

**输出描述**：

**思路**：仍然是并查集，设置了一堆数据结构来处理

~~~c++
#include <iostream>
#include <map>
#include <vector>
#include <cstring>
using namespace std;

const int MAXN = 1000;
int father[MAXN];
int height[MAXN];
int weight[26];

void Initial() {
    for (int i = 0; i < MAXN; i++) {
        father[i] = i;
        height[i] = 0;
    }
    memset(weight, 0, sizeof(weight));
}

int Find(int x) {
    if (x != father[x])
        father[x] = Find(father[x]);
    return father[x];      
}

struct Node {
    int i, weight;
    Node(int a, int b): i(a), weight(b) {}
};
struct Graph {
    int total_w, num;
    Graph(int a, int b): total_w(a), num(b) {}
};

改进：对于字符串可能不同可以考虑使用map映射name和id（看的他人代码）

![image-20230625105954973.png](http://xherlock.top/usr/uploads/2023/06/1549876060.png)

**知识点**

构造方法：**Kruskal**算法和Prim算法，其中Kruskal算法更简单且效率非常高

**算法步骤**：

## 还是畅通工程

**描述**

**输入描述**：

**输出描述**：

对每个测试用例，在1行里输出最小的公路总长度。

本题结果必定有最小生成树，因此不必检查图是否连通

~~~c++
#include <iostream>
#include <algorithm>
#include <map>
using namespace std;

const int MAXN = 100;
int father[MAXN];
int height[MAXN];

struct Edge {
    int node1, node2, dist;
};

bool Compare(Edge x, Edge y) {
    return x.dist < y.dist;
}

void Initial(int n) {
    for (int i = 0; i < n; i++) {
        father[i] = i;
        height[i] = 0;
    }
}

int Find(int x) {
    if (x != father[x])
        father[x] = Find(father[x]);
    return father[x];
}

## 继续畅通工程

**描述**

**输入描述**：

**输出描述**：

每个测试用例的输出占一行，输出全省畅通需要的最低成本。

思路：在上一题基础上结构体Edge增加新的isBuild变量表示路是否修建，Compare重新编写，使得为1的排前面

**注意**：做这道题时发现测试报错，原因在Union里输入的数字应该-1，因为初始化是从0\~N-1

~~~c++
#include <iostream>
#include <algorithm>
#include <map>
using namespace std;

const int MAXN = 100;
int father[MAXN];
int height[MAXN];

struct Edge {
    int node1, node2, cost, isBuild;
};

bool Compare(Edge x, Edge y) {
    if (x.isBuild != y.isBuild)
        return x.isBuild > y.isBuild;
    else
        return x.cost < y.cost;
}

void Initial(int n) {
    for (int i = 0; i < n; i++) {
        father[i] = i;
        height[i] = 0;
    }
}

int Find(int x) {
    if (x != father[x])
        father[x] = Find(father[x]);
    return father[x];
}

int main() {
    int N;
    while (cin >> N) {
        if (N == 0)
            break;
        Initial(N);
        int relation = N * (N - 1) / 2;
        Edge all[relation];
        for (int i = 0; i < relation; i++) {
            cin >> all[i].node1 >> all[i].node2 >> all[i].cost >> all[i].isBuild;   
        }
        sort(all, all + relation, Compare);
        int min_cost = 0;
        for (int i = 0; i < relation; i++) {
            if (Union(all[i].node1-1, all[i].node2-1)) {
                if (all[i].isBuild == 0)
                    min_cost += all[i].cost;
            }
        }
        cout << min_cost << endl;
    }
}
~~~

另外一种思路是，如果遇到isBuild为1，把对应边的长度设置为0也可以

## Freckles

**描述**

**输入描述**：

**输出描述**：

Your program prints a single real number to two decimal places: the minimum total length of ink lines that can connect all the freckles.

思路：题目大意是给出多个坐标，求出连接所有坐标的最小距离

我是把Node转为Edge来做，还是并查集，需要注意数据类型使用double

~~~c++
#include <iostream>
#include <algorithm>
#include <cmath>
#include <iomanip>
using namespace std;

const int MAXN = 100;
int father[MAXN];
int height[MAXN];

struct Edge {
    int node1, node2;
    double dist;
};

struct Node {
    double x, y;
};

bool Compare(Edge x, Edge y) {
    return x.dist < y.dist;
}

void Initial(int n) {
    for (int i = 0; i < n; i++) {
        father[i] = i;
        height[i] = 0;
    }
}

int Find(int x) {
    if (x != father[x])
        father[x] = Find(father[x]);
    return father[x];
}

## Jungle Roads

描述

**输入描述**：

**输出描述**：

思路：题目大意就是给了一堆边，让你找最小连通图

做法完全和前面相同，无非是换了数据结构来存储数据，本方法使用了vector来存储边

~~~c++
#include <iostream>
#include <algorithm>
#include <map>
#include <vector>
using namespace std;

const int MAXN = 26;
int father[MAXN];
int height[MAXN];

struct Edge {
    int node1, node2, dist;
    Edge(int a, int b, int c): node1(a), node2(b), dist(c) {}
};

bool Compare(Edge x, Edge y) {
    return x.dist < y.dist;
}

void Initial(int n) {
    for (int i = 0; i < n; i++) {
        father[i] = i;
        height[i] = 0;
    }
}

int Find(int x) {
    if (x != father[x])
        father[x] = Find(father[x]);
    return father[x];
}

发表评论 取消回复

机试day10

发表评论取消回复