机器学习3

机器学习3

Xherlock

2022 年 08 月 19 日

446 次浏览

暂无评论

1712字数

机器学习

# 机器学习3

## 神经网络

### 非线性假设

使用非线性的多项式能够帮助我们构建更好的分类模型，但是特征太多会导致计算量大增

普通的逻辑回归无法有效处理太多特征，这时需要神经网络

### 神经元和大脑

尝试模仿人类大脑，计算量大（当前计算机足够支持）

![image-20220815090225273.png](http://xherlock.top/usr/uploads/2022/08/2539016669.png)

神经网络原因：现代机器学习应用

### 模型展示

多个输入/树突（dendrite），一个输出/轴突（axon）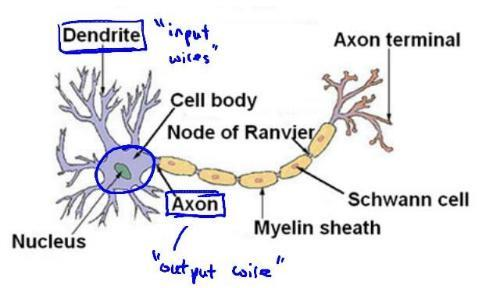

![image-20220815090403351.png](http://xherlock.top/usr/uploads/2022/08/2577395572.png)

神经元（学习模型/激活单元）：多输入一输出，x0称为偏执单元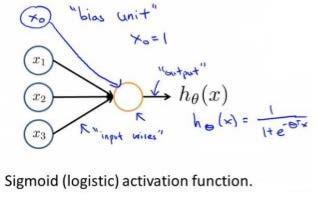

![image-20220815090744511.png](http://xherlock.top/usr/uploads/2022/08/2601673770.png)

在神经网络中把&theta;向量称为权重

神经网络图如下：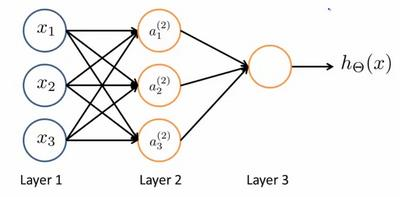

![image-20220815091037357.png](http://xherlock.top/usr/uploads/2022/08/4216712938.png)

分别为输入层、隐藏层、输出层：隐藏层用来计算复杂特征

为每一层增加一个偏差单位（bias unit）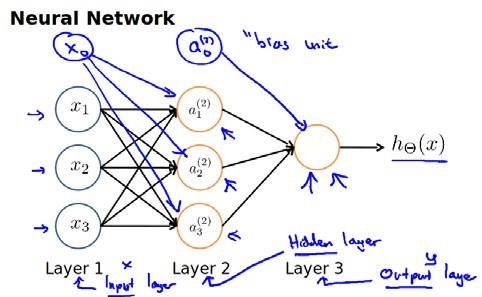

![image-20220815091526029.png](http://xherlock.top/usr/uploads/2022/08/4240317245.png)

此时$a_i^{(j)}$代表第j层的第i个激活单元，$\theta^{(j)}$代表从第j层映射到第j+1层的权重矩阵；则上图的激活单元和输出分别表达为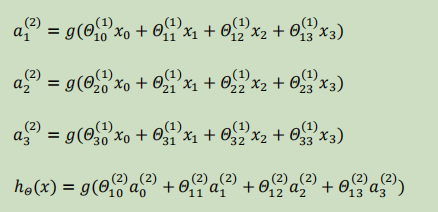

![image-20220815091739981.png](http://xherlock.top/usr/uploads/2022/08/3604611105.png)

$\theta^{(j)}$为$s_{j+1}\times(s_j+1)$维度，即第j+1层单元数乘以第j层单元数+1【偏差单元】的和

### 例子与直观理解

**逻辑与**（and）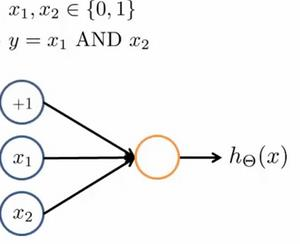

![image-20220815122318471.png](http://xherlock.top/usr/uploads/2022/08/1439330799.png)

eg：&theta;0=-30, &theta;1=20, &theta;2=20

h&theta;(x) = g(−30 + 20x1 +20x2)

**逻辑或**（or）

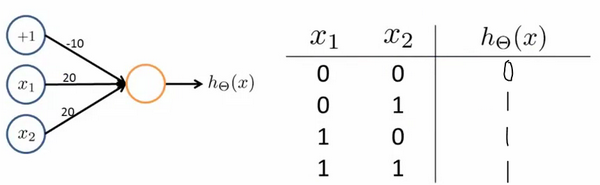![image-20220815171620661](http://xherlock.top/usr/uploads/2022/08/2373797585.png)

**逻辑非**（not）

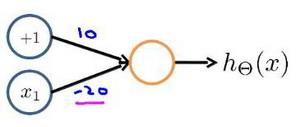![image-20220815171731560](http://xherlock.top/usr/uploads/2022/08/2694495701.png)

**异或**（xor）

XNOR = (x1 AND x2) OR((NOT x1)AND(NOT x2))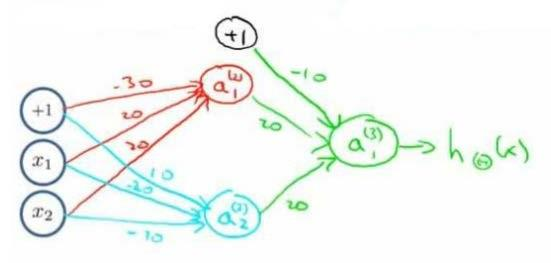

![image-20220815172141591](http://xherlock.top/usr/uploads/2022/08/1215834646.png)

### 多元分类

eg：每个向量中为1的为一类

![image-20220815172759644](http://xherlock.top/usr/uploads/2022/08/3412388558.png)

### 代价函数

最后修改：2022 年 08 月 19 日

如果觉得我的文章对你有用，请随意赞赏

机器学习3

Xherlock • 2022 年 08 月 19 日

发表评论取消回复

Reverse（十一）

Win11新机鼓捣记录

C++学习

栈~数制转换

Python实现文件管理系统（重命名和删除）

机器学习1

Python爬取壁纸

计算机系统概述

数字签名

美化和集成控制台

机器学习3

发表评论 取消回复

机器学习3

发表评论取消回复