机器学习2

机器学习2

Xherlock

2022 年 08 月 19 日

406 次浏览

暂无评论

1905字数

机器学习

# 机器学习2

## 逻辑回归

### 代价函数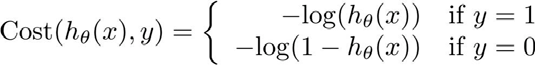

![image-20220814084619377.png](http://xherlock.top/usr/uploads/2022/08/1421421815.png)

so，$J(\theta)=\frac{1}{m}\sum_{i=1}^mCost(h_{\theta}(x),y)$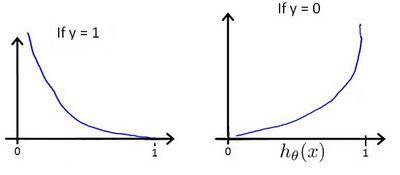

![image-20220814084950382.png](http://xherlock.top/usr/uploads/2022/08/2152589204.png)

实现一个完整的逻辑回归算法：

上面的$Cost(h_{\theta}(x),y)$可以简化为$Cost(h_{\theta}(x),y)=-y*log(h_{\theta}(x))-(1-y)*log(1-h_{\theta}(x))$

即$J(\theta)=-\frac{1}{m}\sum_{i=1}^m[y^{(i)}*log(h_{\theta}(x^{(i)}))+(1-y^{(i)})*log(1-h_{\theta}(x^{(i)}))]$

要找到使J(&theta;)最小的&theta;，

### 高级优化

共轭梯度法（conjugate gradient）、L-BGFS、BFGS算法：优化代价函数

**优点**：不需手动选择学习率（线性搜索算法，自动尝试不同的学习率），收敛速度远快于梯度下降

### 多元分类：一对多

类别&gt;2时，需要考虑如何多分类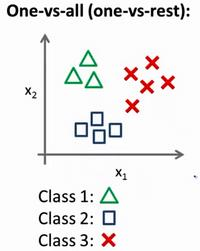

![image-20220814093543046.png](http://xherlock.top/usr/uploads/2022/08/3237158920.png)

一类 和 其他所有类分为一类，分别得出预测函数

![image-20220814093800352.png](http://xherlock.top/usr/uploads/2022/08/1288003071.png)

## 正则化

### 过拟合问题(overfitting)

**线性回归问题**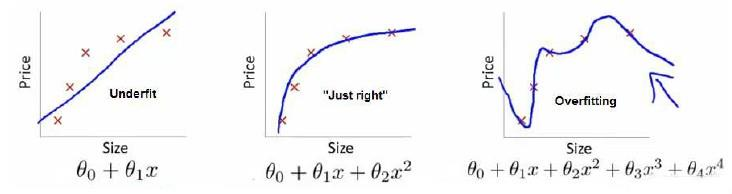

![image-20220814165501217.png](http://xherlock.top/usr/uploads/2022/08/1114084364.png)

第三个就是过拟合（拟合所有数据点）

**分类问题**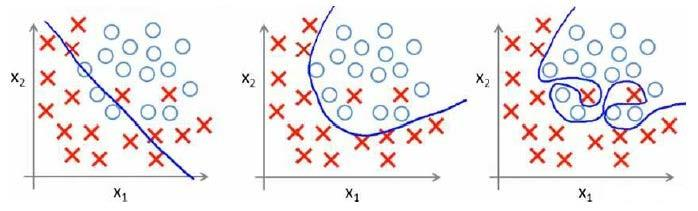

![image-20220814165705237.png](http://xherlock.top/usr/uploads/2022/08/2797047113.png)

如何解决过拟合？

* 特征变量少时可以通过绘图来分辨
* 减少特征变量数目
* 正则化（保留所有特征，但是减少参数的大小）

### 代价函数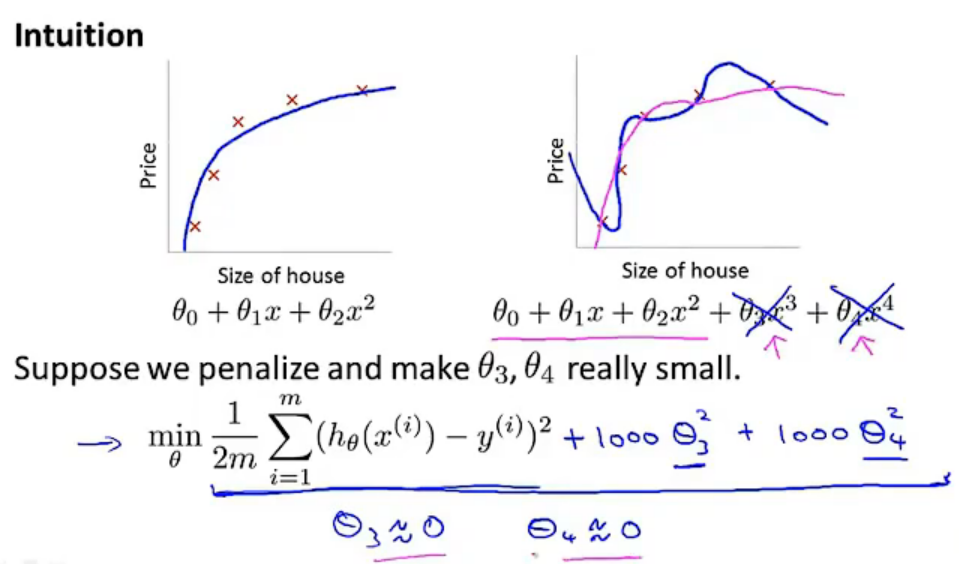

![image-20220814170321795.png](http://xherlock.top/usr/uploads/2022/08/2017152992.png)

惩罚项&theta;3，&theta;4，使它们尽可能小

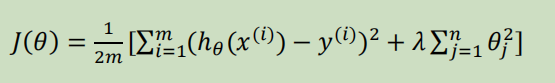![image-20220814170633458.png](http://xherlock.top/usr/uploads/2022/08/3976800764.png)

$\lambda$称为正则化参数（**Regularization Parameter**），太大会导致使所有参数都最小化，导致模型变成类似于一条水平直线，这样不合适

### 线性回归的正则化

化简后得到：前半部分接近于$\theta_j$，后半部分和未正则化一样

![image-20220814171321507.png](http://xherlock.top/usr/uploads/2022/08/4028724194.png)

也可以利用正规方程来求解正则化线性回归模型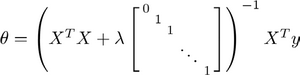

![image-20220814171916641.png](http://xherlock.top/usr/uploads/2022/08/3131469137.png)

### 逻辑回归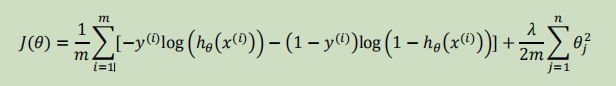

![image-20220814172142125.png](http://xherlock.top/usr/uploads/2022/08/1427145877.png)

最后修改：2022 年 08 月 19 日

如果觉得我的文章对你有用，请随意赞赏

机器学习2

Xherlock • 2022 年 08 月 19 日

发表评论取消回复

Reverse（十一）

Win11新机鼓捣记录

栈~数制转换

C++学习

Python实现文件管理系统（重命名和删除）

《加密与解密》-逆向分析技术

Reverse（五）

链路层（一）

推荐工具软件和浏览器插件

网络层（一）

机器学习2

发表评论 取消回复

机器学习2

发表评论取消回复