分组密码（一）

概述

明文消息编码后的二元数字序列为M={x$_{0}$,x$_{1}$,…,x$_{k}$, …}，分组密码首先将 M 划分成长为 m 的组块 B$_{i}$ ＝(x$_{i × m}$ ,x$_{i × m +1}$ ,…,x $_{i × m + m - 1}$ )(长为 m 的向量)的集合，然后各组分别在密钥 K 的控制下变换成长 度为 n 的组块 C$_{i}$＝(y$_{i×n}$，y$_{i×n+1}$,…,y$_{i×n+n-1}$)(长为 n 的向量)

  • n>m：有数据扩展的分组密码
  • n<m：有数据压缩的分组密码
  • n=m：无数据扩展和压缩的分组密码

分组密码的数学模型：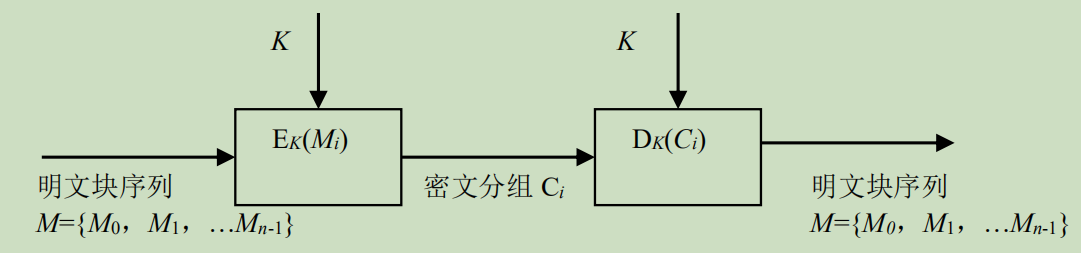

image-20220303204129090.png

分组密码特点：速度快、易于标准化和便于软硬件实现等，在计算机通信和信息系统安全领域有着最广泛的应用

分组密码的设计原则与评估

分组密码的设计原则

  1. 针对安全性的一般涉及原则：

    • 分组长度和密钥长度：明文分组和密钥长度尽可能大
    • 扰乱原则：设计的密码应使得密钥和明文以及密文之间的依赖关系相当复杂，以至于这种依赖型对密码分析者来说是无法利用的
    • 扩散原则：设计的密码应使得密钥的每一位影响密文的许多位以防止对密钥进行逐段破译，而且明文的每一位也应影响密文的多位以便隐蔽明文的统计特性

  2. 针对实现的设计原则：

    • 软件实现的设计原则：使用子块和简单的运算
    • 硬件实现的设计原则：尽量使用规则结构
  3. 分组密码的评估

安全性：

  • 算法抗密码分析的强度
  • 可靠的数学基础
  • 算法输出的随机性
  • 与其他算法比较的相对安全性

性能：在各种平台上的计算效率和对存储空间的需求

算法和实现特性：灵活性、硬件和软件适应性、算法的简单性

分组密码设计方法

SPN结构

采用SPN的密码有SAFER、SHARK、AES等

第一层为S层：也称替换层，主要起扰乱作用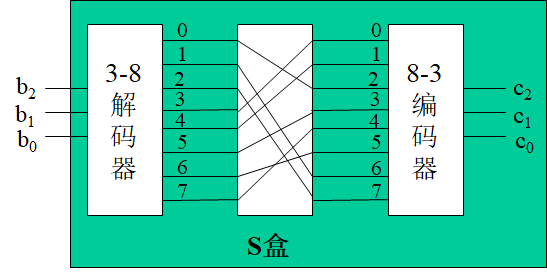

image-20220310210122150.png

第二层为P层，也称置换层，主要起扩散作用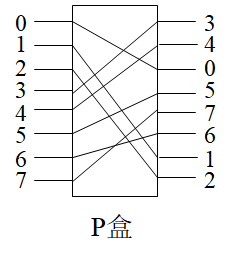

image-20220310210047737.png

一轮SPN型密码加密过程

image-20220310212743437

Feistel结构

采用Feistel的分组密码有Blowfish、RC5、DES等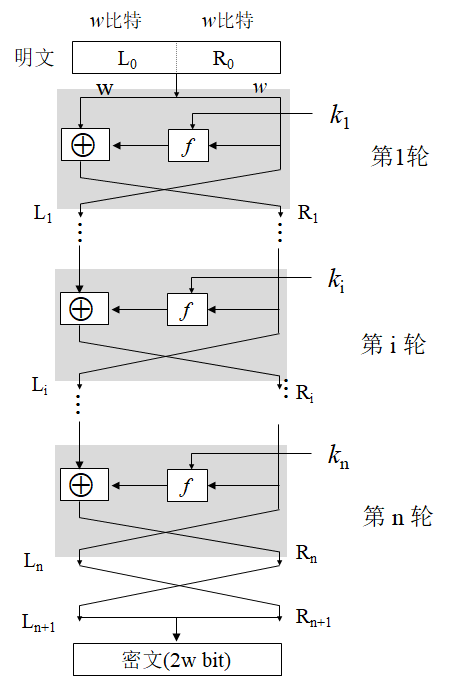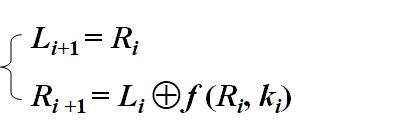

image-20220323102322326.png

image-20220323095821857.png

结构特点

  • 输入为2w比特的分组（称为左半分组和右半分组）
  • 函数F用于产生扩散和混淆作用，但把并不要求为可逆函数
  • $k_{i}$为由密码密钥K生成的子密钥
  • Feistel网络由n个基本结构单元构成（$k_{i}$互不相同）

Feistel结构实现依赖：

  • 分组大小：越大安全性越高，但运算速度越慢，一般64位
  • 密钥长度：越大安全性越高，但运算速度越慢，一般128位
  • 循环次数：越多安全性越高，但运算开销越大，通常采用16次
  • 子密钥产生算法：算法越复杂越难分析
  • 轮函数F：复杂性越高越难分析

数据加密标准DES

概述

美国发布，用于保护计算机数据，由IBM研制，现在已经逐步退出历史舞台，但其促进了分组密码设计与分析的发展

DES是一种分组加密算法，明文分组、输出密文、密钥长度均为64位，有效密钥为56为（8位用于奇偶校验）。由初始置换、16轮迭代、初始逆置换组成（Feistel密码算法）

运行一次只能加密64位长度的数据，处理大量数据需要花费很长事件，不适合大数据处理；同时DES属于对称加密算法，使用相同的密钥进行加密和解密

基本运算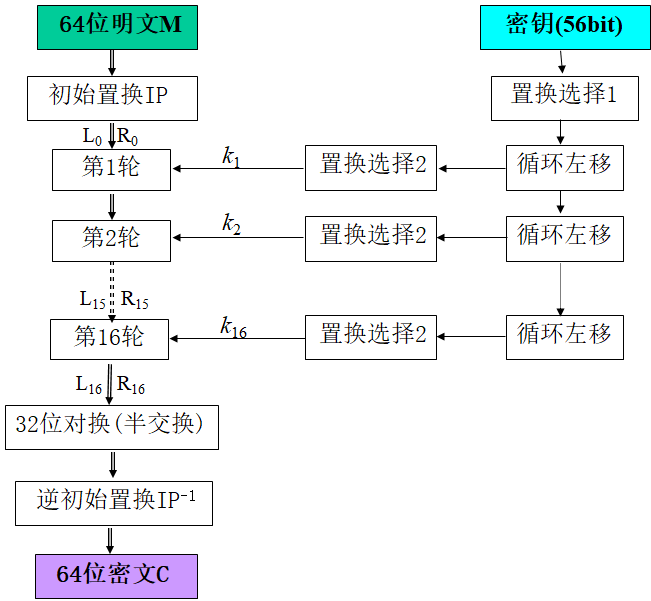

image-20220323103109828.png

加密流程

  1. 输入明文以64位一组进行初始置换
  2. 将初始置换后的结果均分为$L_{0}$和$R_{0}$两组
  3. 64位密钥K经过变换成为48位子密钥$k_{1}$和32位的$R_{0}$（E扩展为48位）输入F函数进行处理，输出32位处理结果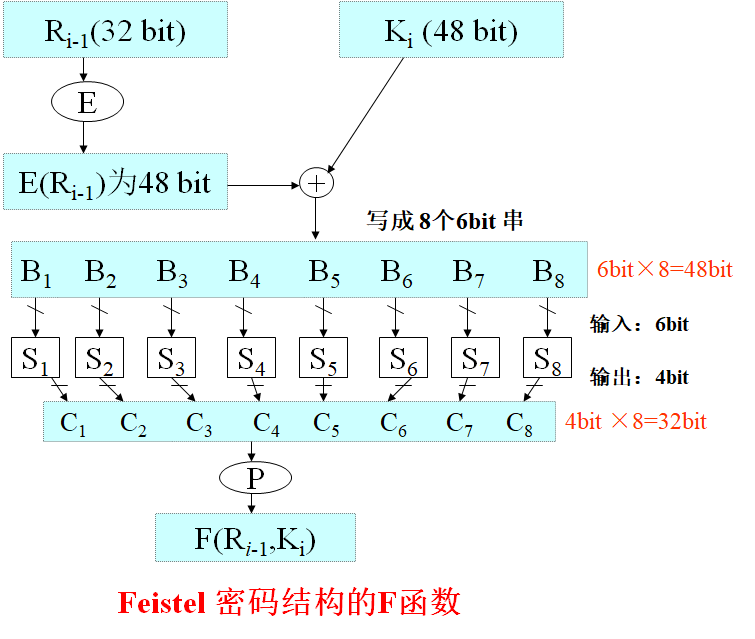

image-20220323104918294.png

  1. 将32位F函数处理结果与32位的$L_{0}$进行按位异或后赋给$R_{1}$，$R_{0}$赋给$L_{1}$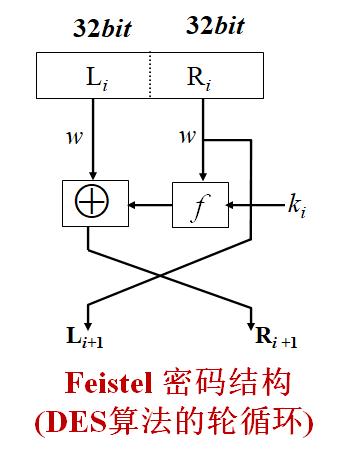

image-20220323110357337.png

  1. 重复3，4步16轮最后得到$L_{16}$和$R_{16}$
  2. 将二者对换合并得到64位数据
  3. 对64位数据进行逆初始值置换得到密文

详细步骤

  1. 初始置换IP表和初始逆置换IP$^{-1}$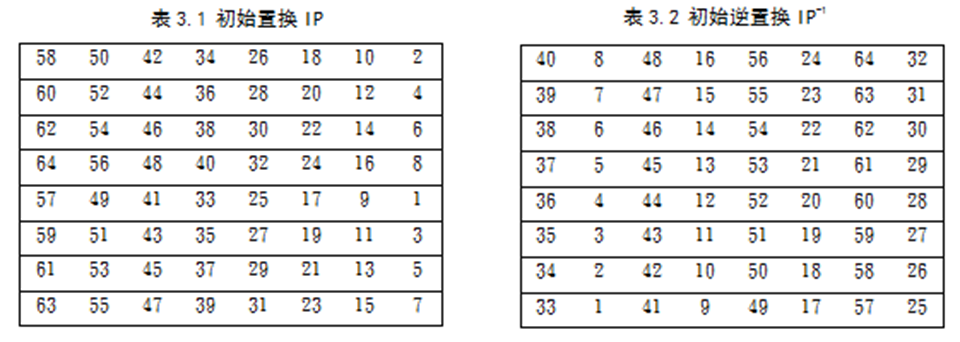

image-20220323112046812.png

将64位明文8*8排好，第58位bit放到第一位，以此类推；密文同样如此生成

  1. LR分组

实际是按照8*8表格上下进行分组，称为左右（实际就是前32位给左表，后32位给右表）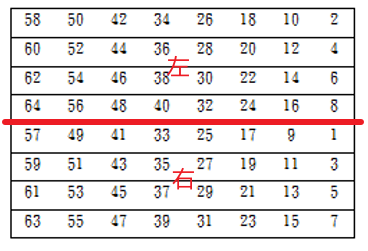

image-20220323113209621.png

  1. F函数处理

    • E-扩展运算：中间为原始数据，左右两列为新扩展的数据（新扩展的数据可以有效地影响很多位，同时能够与密钥进行异或运算）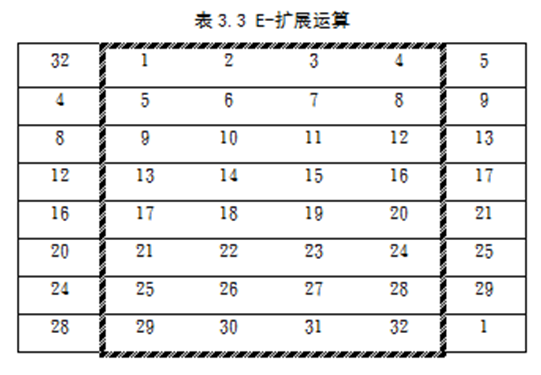

    image-20220323113504055.png

    • S-盒置换：48位异或后的结果分成8组×6bits，每组分别进行处理，使得输入6bits，输出4bits，结构如图（实际1-8盒不同的）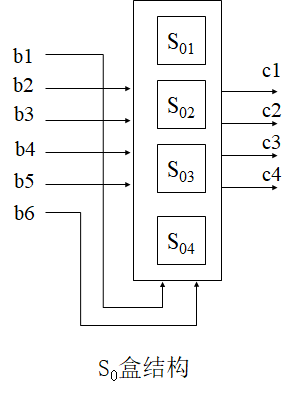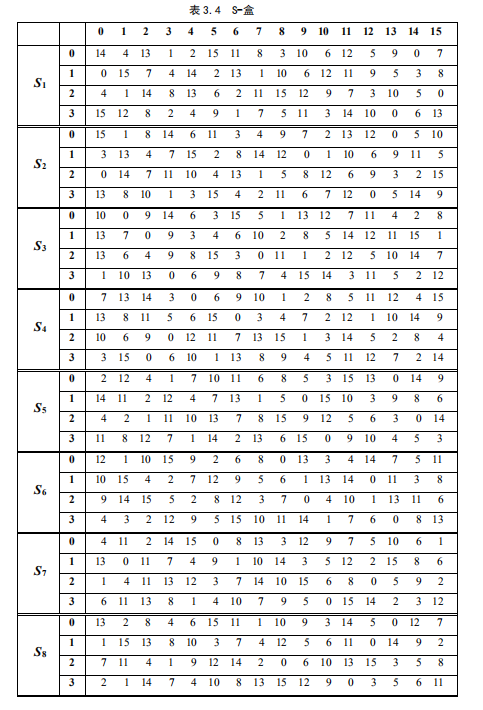

    image-20220323114332030.png

    image-20220323114934980.png

    每个S盒都是6位的输入，4位的输出。$(h_{1}…h_{6})$的值就是对应表$S_{i}(h_{1}h_{6})_{2}$行和$(h_{2}h_{3}h_{4}h_{5})_{2}$列的值，eg：

    image-20220323221755284.png

    输入100101即为第4行第3列的1000--8

    S盒的设计特点

    • 任何S盒都不是输入变量的线性函数
    • 改变S盒的1个输入位，至少引起2位的输出变化
    • 任何一个S盒，如果固定一个输入位，其他输入变化时，输出数字中0和1的总数近于相等
    • P置换

    同初始置换类似，只是打乱数据位置，对8个S盒的输出进行变换，实现扩散效果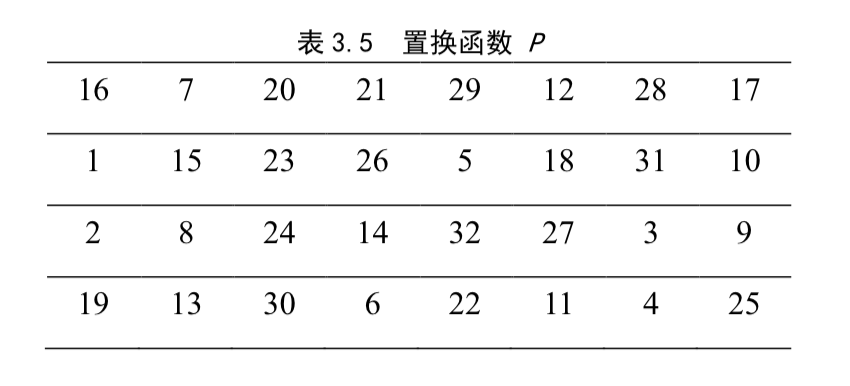

    26644676E50DA765EB697AC3EF22836E.png

  3. F函数输出的32位数据与$L_{i}$组数据进行安慰异或运算，得到结果赋给$R_{i+1}$，$R_{i}$组32位数据赋给$L_{i+1}$完成一轮循环，之后继续循环操作直至得到$L_{16}$和$R_{16}$，并实现合并
  4. 合并后的64位数据按逆初始值置换表处理
  5. 子密钥生成：初始密钥64位，其中奇偶检验8位（第8、16、24、32、40、48、56、64位丢弃），有效位56位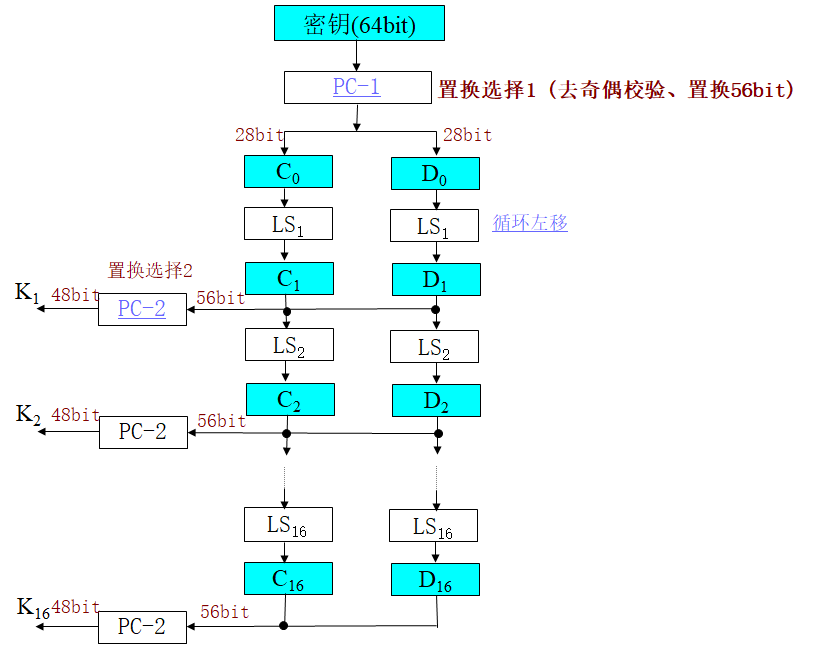

image-20220324082801467.png

  • 64位$\rightarrow$56位数据利用固定的置换PC-1置换得到$C_{i}$和$D_{i}$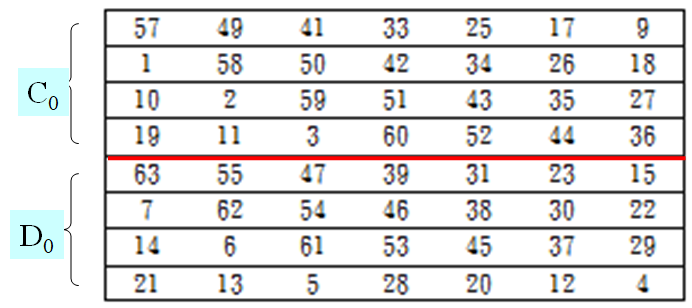

    image-20220324082559095.png

  • 56位$\rightarrow$48位数据利用固定的置换PC-2置换（第9、18、22、25、35、38、43、54位丢弃）得到$K_{i}$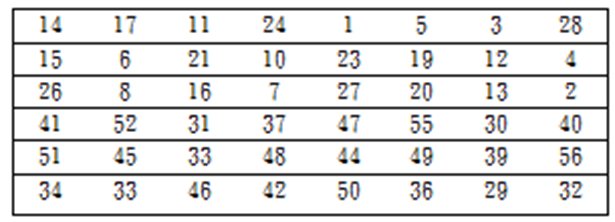

    image-20220324082640464.png

  • $LS_{i}$表示1个或2个位置的左循环移位

    image-20220324083209188.png

最后修改：2022 年 03 月 24 日
© 允许规范转载
如果觉得我的文章对你有用，请随意赞赏