古典密码技术
替代密码（Substitution Cipher）
先建立一个替换表，加密时依次替换字符
按照密码算法加解密时使用替换表多少分类如下
graph LR
A[替代密码]-->B[单表替代密码]
A[替代密码]-->C[多表替代密码]单表替代密码
一般单表替代密码
原理
以26个英文字母集合上的一个置换π为密钥，对明文消息中的每个字母依次进行变换
明文m，密文c，定义
加密变换：$e_{\pi}(m)=\pi(m)=c$
解密变换：$d_{\pi}(c)=\pi^{-1}(c)=m$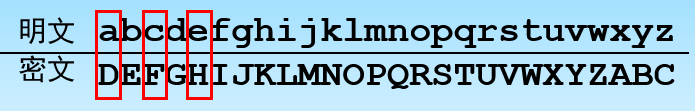
graph LR
A[xherlock]-->B[AKHUORFN]特点
- 密钥空间K很大，使用穷举法几乎不可行
- 移位密码体制时其中的一个特例，仅含26个置换
- 密钥π不便于记忆
移位密码
原理
特点
k=3时，是凯撒密码
仿射密码
原理
密钥短语密码
原理
选用一个英文短语或单词串作为密钥，去掉其中重复的字母得到一个无重复字母的字符串，然后再将字母表中的其他字母依次写于此字母串后，即可构造出一个字母替代表
单表替代密码安全性
不足：属于单字母一一对应，没有将明文字母出现得概率隐藏起来，再实际应用中，可利用自然语言的统计特性来破译此类密码，如下表
| 字母 | 出现频率 | 字母 | 出现频率 |
|---|---|---|---|
| a ③ | 0.0856 | n ⑤ | 0.0707 |
| b | 0.0139 | o ④ | 0.0797 |
| c | 0.0279 | p | 0.0199 |
| d | 0.0378 | q | 0.0012 |
| e ① | 0.1304 | r ⑥ | 0.0677 |
| f | 0.0289 | s | 0.0607 |
| g | 0.0199 | t ② | 0.1045 |
| h | 0.0528 | u | 0.0249 |
| i ⑦ | 0.0627 | v | 0.0092 |
| j | 0.0013 | w | 0.0149 |
| k | 0.0042 | x | 0.0017 |
| l | 0.0339 | y | 0.0199 |
| m | 0.0249 | z | 0.0008 |
多表替代密码
将明文字母划分为长度相同的单元，称为明文分组，这样可以使同一字母有不同的密文
特点：使用了两个或两个以上的替代表
维吉尼亚密码
原理
希尔密码
原理
将n个敏文字母通过线性变换，转换为n个密文字母
特点
- 可以很好的抑制自然语言的统计特性，具有较高安全强度
- 密钥空间较大
- 易受已知明文攻击及选择明文攻击
一次一密码
原理
替代密码的密钥是一个随机且不重复的字符序列，也称Vernam密码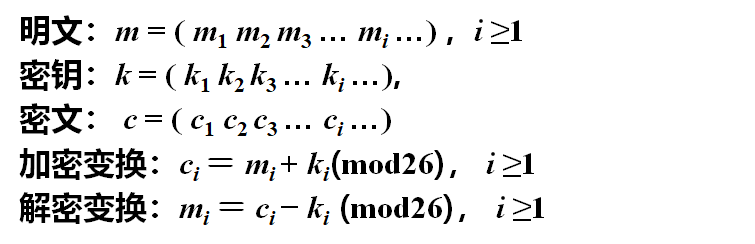
要求：密钥随机产生，且只能用一次
但在实际中很难保证密钥的安全性，因为密钥有产生、存储、分发的过程，同时密钥长度可能会很长（因为得大于等于明文得长度）
Playfair密码
原理
双字母单表替代密码，将明文中的栓字母作为一个单元对待，并将这些单元转换为密文字母组合，下表是密码字母矩阵
| p | l | a | y | f |
|---|---|---|---|---|
| i /j | r | s | d | g |
| m | c | h | e | b |
| k | n | o | q | t |
| u | v | w | x | z |
加密规则：取双字母分别为P1、P2
- 若P1、P2在同一行，密文C1、C2分别是紧靠P1、P2右端的字母；
- 若P1、P2在同一列，密文C1、C2分别是紧靠P1、P2下方的字母；
- 若P1、P2不在同一行，也不在同一列，则C1、C2是由P1、P2确定的矩形其它两角的字母，且C1和P1在同一行，C2和P2在同一行；
- 若P1＝P2，则两个字母间插入一个预先约定的字母，如x，并用前述方法处理；如balloon，则以ba lx lo on 来加密。
- 若明文字母数为奇数，则在明文尾填充约定字母。
算法还约定字母矩阵中第一列看做最后一列的右边一列，
表中第一行看做最后一行的下一行。
特点
- 组合多，频率分析困难
置换密码（Permutation Cipher）
通过改变明文消息各元素的相对位置，但明文消息元素本身的取值或内容形式不变
周期置换密码
特点
将明文字符按一定长度n分组，把每组的字符按1、2……n的一个置换π重排位置次序来得到密文，密钥即为置换π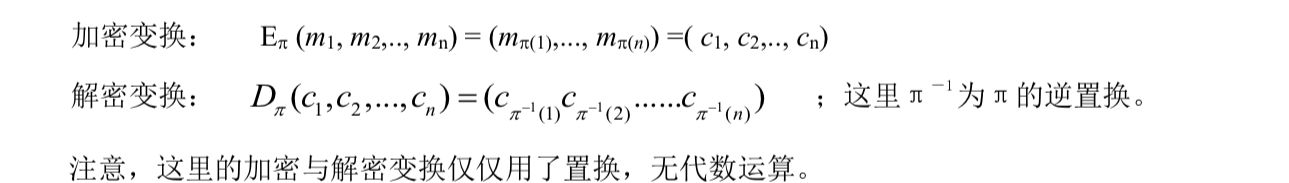
置换密码在实质上是Hill密码的特例
列置换密码
转轮机密码
历史上著名的恩尼格玛
