机试day8

博主： Xherlock
发布时间：2023 年 06 月 12 日
316 次浏览
暂无评论
777字数
分类： C/C++&机试

# 机试day8

## 最大公约数

[最大公约数_牛客题霸_牛客网 (nowcoder.com)](https://www.nowcoder.com/practice/20216f2c84bc438eb5ef05e382536fd3?tpId=40&tqId=21492&tPage=8&rp=8&ru=/ta/kaoyan&qru=/ta/kaoyan/question-ranking)

**描述**

输入两个正整数，求其最大公约数。

**输入描述**：

测试数据有多组，每组输入两个正整数。

**输出描述**：

对于每组输入,请输出其最大公约数。

思路：辗转相除法，也可以写个递归的取模函数

~~~c++
#include <iostream>
using namespace std;

int main() {
    int a, b;
    while (cin >> a >> b) {
        int tmp;
        while (b) {
            tmp = a % b;
            a = b;
            b = tmp;
        }
        cout << a << endl;
    }
}
~~~

## 最简真分数

[最简真分数_牛客题霸_牛客网 (nowcoder.com)](https://www.nowcoder.com/practice/1f1db273eeb745c6ac83e91ff14d2ec9?tpId=61&tqId=29507&tPage=1&ru=%2Fkaoyan%2Fretest%2F1002&qru=%2Fta%2Fpku-kaoyan%2Fquestion-ranking)

**描述**

给出n个正整数，任取两个数分别作为分子和分母组成最简真分数，编程求共有几个这样的组合。

**输入描述**：

每组包含n（n<=600）和n个不同的整数，整数大于1且小于等于1000。

**输出描述**：

每行输出最简真分数组合的个数。

思路：转换为求最大公约数，如果不为1，则为最简真分数

~~~c++
#include <iostream>
using namespace std;

int is_zuijian(int a, int b) {
    int tmp;
    while (b) {
        tmp = a % b;
        a = b;
        b = tmp;
    }
    if (a != 1)
        return 0;
    else
        return 1;
}

int main() {
    int n;
    while (cin >> n) {
        if (n == 0)
            break;
        int num[n];
        for (int i = 0; i < n; i++) {
            cin >> num[i];
        }
        int m = 0;
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                m += is_zuijian(num[i], num[j]);
            }
        }
        cout << m << endl;
    }
}
~~~

## 素数判定

[素数判定_牛客题霸_牛客网 (nowcoder.com)](https://www.nowcoder.com/practice/5fd9c28b1ce746dd99287a04d8fa9002?tpId=40&tqId=21494&tPage=8&rp=8&ru=%2Fta%2Fkaoyan&qru=%2Fta%2Fkaoyan%2Fquestion-ranking)

**描述**

给定一个数n，要求判断其是否为素数（0,1，负数都是非素数）。

**输入描述**：

测试数据有多组，每组输入一个数n。

**输出描述**：

对于每组输入,若是素数则输出yes，否则输入no。

思路：对于大于1的数遍历取模，若余数为0，说明存在银子，不是质数【巧妙方法：比到根号n即可，数论知识】

~~~c++
#include <iostream>
#include <math.h>
using namespace std;

int is_prime(int n) {
    int prime = 1;
    for (int i = 2; i <= sqrt(n); i++) {
        if (n % i == 0) {
            prime = 0;
            break;
        }
    }
    return prime;
}

int main() {
    int n, prime;
    while (cin >> n) {
        if (n <= 1)
            prime = 0;
        else {
            prime = is_prime(n);
        }
        if (prime)
            cout << "yes" << endl;
        else
            cout << "no" << endl;
    }
}
~~~

## 素数

[素数_牛客题霸_牛客网 (nowcoder.com)](https://www.nowcoder.com/practice/7f4be54b37a04fdaa4ee545819151114?tpId=66&tqId=29630&tPage=1&ru=/kaoyan/retest/1004&qru=/ta/buaa-kaoyan/question-ranking)

**描述**

输入一个整数n(2<=n<=10000)，要求输出所有从1到这个整数之间(不包括1和这个整数)个位为1的素数，如果没有则输出-1。

**输入描述**：

输入有多组数据。 每组一行，输入n。

**输出描述**：

输出所有从1到这个整数之间(不包括1和这个整数)个位为1的素数(素数之间用空格隔开，最后一个素数后面没有空格)，如果没有则输出-1。

思路：本题无非就是多了个要求**素数个位为1**，直接for循环从11每次加10，每个循环内做一次上一题的is_prime判断

~~~c++
#include <iostream>
#include <math.h>
using namespace std;

int is_prime(int n) {
    int prime = 1;
    for (int i = 2; i <= sqrt(n); i++) {
        if (n % i == 0) {
            prime = 0;
            break;
        }
    }
    return prime;
}

int main() {
    int n, has_prime;
    while (cin >> n) {
        has_prime = 0;
        for (int i = 11; i < n; i += 10) {
            if (is_prime(i)) {
                has_prime++;
                cout << i << ' ';
            }
        }
        if (!has_prime)
            cout << "-1";
        cout << endl;
    }
}
~~~

瞅了眼题解，发现个搞笑的：他的做法和id很搭配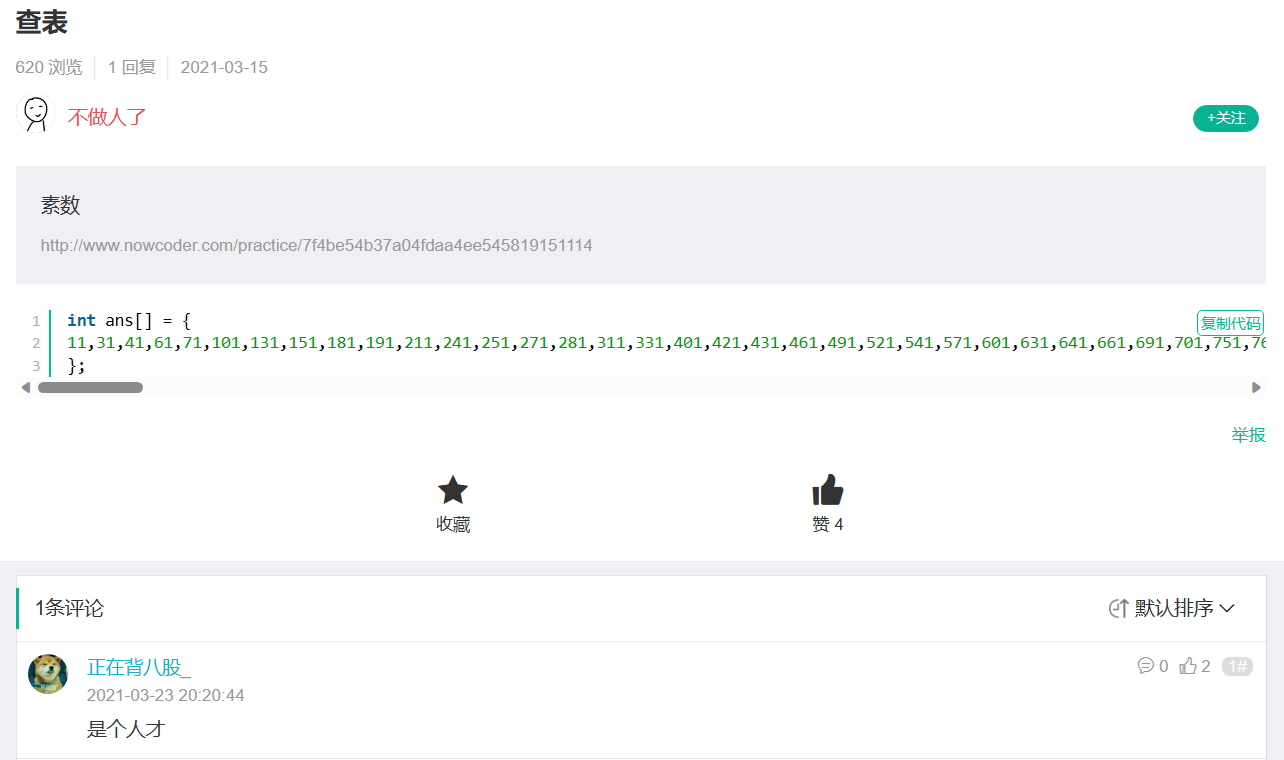

![image-20230610171646980.png](http://xherlock.top/usr/uploads/2023/06/3741874374.png)

## Prime Number

[Prime Number_牛客题霸_牛客网 (nowcoder.com)](https://www.nowcoder.com/practice/c5f8688cea8a4a9a88edbd67d1358415?tpId=62&tqId=29467&tPage=1&ru=/kaoyan/retest/2002&qru=/ta/sju-kaoyan/question-ranking)

**描述**

Output the k-th prime number.

**输入描述**：

k≤10000

**输出描述**：

The k-th prime number.

思路：本题依然很简单，为了应对不同可能的k值，我们可以提前先找好10000个素数存入vector，直接下标k取值就好

做了一个加速【感觉不明显】，首先已经存好2，剩下的只检查奇数

~~~c++
#include <iostream>
#include <vector>
#include <math.h>
using namespace std;

int is_prime(int n) {
    int prime = 1;
    for (int i = 2; i <= sqrt(n); i++) {
        if (n % i == 0) {
            prime = 0;
            break;
        }
    }
    return prime;
}

int main() {
    vector<int> prime_number;
    prime_number.push_back(2);
    int i = 3;
    while (prime_number.size() <= 10000) {
        if (is_prime(i))
            prime_number.push_back(i);
        i += 2;
    }
    int k;
    while (cin >> k) {
        cout << prime_number[k-1] << endl;
    }
}
~~~

额外学习下：埃氏筛法

**埃氏筛法**：用已经筛选出的素数去过滤所有能整除它的数，但是只能在给定范围内快速筛选，所需时间少很多

~~~c++
const int maxn = 10000000;
int prime[maxn];
bool IsPrime[maxn];//0代表都是素数
void Find_Prime(){
    IsPrime[1] = 1;//1不是素数
    int pNum = 0;
    for(int i = 2; i <= maxn; i++){
        if(!IsPrime[i]){
            prime[pNum++] = i;  
        }
        for(int j = 0; j < pNum && i * prime[j] <= maxn; j++){
            IsPrime[i * prime[j]] = 1;
            if(i % prime[j] == 0){
                break;
            }
        }
    }
}
~~~

## 质因数的个数

[质因数的个数_牛客题霸_牛客网 (nowcoder.com)](https://www.nowcoder.com/practice/20426b85f7fc4ba8b0844cc04807fbd9?tpId=60&tqId=29479&tPage=1&ru=/kaoyan/retest/1001&qru=/ta/tsing-kaoyan/question-ranking)

**描述**

求正整数N(N>1)的质因数的个数。 相同的质因数需要重复计算。如120=2*2*2*3*5，共有5个质因数。

**输入描述**：

可能有多组测试数据，每组测试数据的输入是一个正整数N，(1<N<10^9)。

**输出描述**：

对于每组数据，输出N的质因数的个数。

思路：完全没必要用书上的先求一定范围素数，在一个个遍历

可以从2开始，一个个去除N，每遇到一个余0的num++，直到N完全没有该因子

~~~c++
#include <iostream>
using namespace std;

int main() {
    int N;
    while (cin >> N) {
        int num = 0;
        int factor = 2;
        while (N != 1) {
            while (N % factor == 0) {
                N /= factor;
                num++;
            }
            factor++;
        }
        cout << num << endl;
    }
}
~~~

## 约数的个数

**描述**

输入n个整数,依次输出每个数的约数的个数

**输入描述**：

输入的第一行为N，即数组的个数(N<=1000) 接下来的1行包括N个整数，其中每个数的范围为(1<=Num<=1000000000)

**输出描述**：

可能有多组输入数据，对于每组输入数据， 输出N行，其中每一行对应上面的一个数的约数的个数。

### 法1：偏暴力搜索

思路：由欧拉函数知，一个合数的因数数目为所有素因数数目+1的乘积，例如$6=2\times3$，即6有$(1+1)\times(1+1)=4$个因数，$12=2^2\times3$，即12有$(2+1)\times(1+1)=6$个因数，以此方式计算约束个数

但是由于需要找出素因数，会耗费不少时间（假如N很大，factor++这里循环较长时间），导致程序超时【当然有解决办法，即提前算好素因数】

~~~c++
#include <iostream>
#include <vector>
#include <cmath>
using namespace std;

int main() {
    int N;
    while (cin >> N) {
        int num[N];
        for (int i = 0; i < N; i++) {
            cin >> num[i];
            int factor = 2;
            vector<int> M;
            while (num[i] != 1) {
                int factor_num = 0;
                while (num[i] % factor == 0) {
                    num[i] /= factor;
                    factor_num++;
                }
                if (factor_num)
                    M.push_back(factor_num + 1);
                factor++;
            }
            int result = 1;
            for (int i = 0; i < M.size(); i++) {
                result *= M[i];
            }
            cout << result << endl;
        }
    }
}
~~~

### 法2：因数成对出现

除了完全平方数外，都是成对出现，因此只需计算到$\sqrt{n}$即可，每次+2，如果完全平方数中间+1

~~~c++
#include <iostream>
#include <vector>
#include <cmath>
using namespace std;

int main() {
    int N;
    while (cin >> N) {
        int num[N];
        for (int i = 0; i < N; i++) {
            cin >> num[i];
            int result = 0, j;
            for (j = 1; j < sqrt(num[i]); j++) {
                if (num[i] % j == 0) {
                    result += 2;
                }  
            }
            if (num[i] == j * j)
                result++;
            cout << result << endl;
        }
    }
}
~~~

## 整除问题

[整除问题_牛客题霸_牛客网 (nowcoder.com)](https://www.nowcoder.com/practice/8e29045de1c84d349b43fdb123ab586a?tpId=62&tqId=29462&tPage=1&ru=/kaoyan/retest/2002&qru=/ta/sju-kaoyan/question-ranking)

**描述**

给定n，a求最大的k，使n！可以被a^k整除但不能被a^(k+1)整除。

**输入描述**：

两个整数n(2<=n<=1000)，a(2<=a<=1000)

**输出描述**：

一个整数.

思路：首先本题目肯定**无法使用一般数字类型**，因为n的阶乘太大；因此需要结合因数拆解来做

这里有一些学网安数当时的味，发现很多当时学的完全可以用到现在这里

这道题根本上还是得去做因式分解，文字不好描述，直接上案例：设a=12，则$12=2^2\times3$，我们要做的是找到n的阶乘结果中包含了多少个2和3因数，假设含有i个2和j个3，那么k应该是i/2和j中最大的结果

首先还是获取1000以内的素数，使用模板！！！记住它

~~~c++
const int MAXN = 1001;
vector<int> prime;
bool isPrime[MAXN];

void getPrime() {
    memset(isPrime, true, sizeof(isPrime));
    isPrime[0] = false;
    isPrime[1] = false;
    for (int i = 2; i < MAXN; i++) {
        if (!isPrime[i]) {
            continue;
        } else {
            prime.push_back(i);
            for (int j = i * i; j < MAXN; j += i) {
                isPrime[j] = false; 
            }
        }
    }
}
~~~

getBiggestPrimeFactor用来获取a的最大素因数及其指数，getFactorNum获取n的阶乘中含有最大素因数个数

~~~c++
pair<int, int> getBiggestPrimeFactor(int a) {
    int upper_bound = sqrt(a) + 1;
    pair<int, int> biggestPrimeFactor = make_pair(1, 0);
    for (int i = 0; i < a && i < upper_bound; i++) {
        int factor = prime[i];
        int index = 0;
        while (a % factor == 0) {
            a /= factor;
            index++;
        }
        if (a == 1) {
            biggestPrimeFactor.first = factor;
            biggestPrimeFactor.second = index;
            break;
        }
    }
    if (a > 1) {
        biggestPrimeFactor.first = a;
        biggestPrimeFactor.second = 1;
    }
    return biggestPrimeFactor;
}

int getFactorNum(int n, int factor) {
    return n == 0? 0: n / factor + getFactorNum(n / factor, factor);
}

int main() {
    getPrime();
    int a, n;
    while (cin >> n >> a) {
        pair<int ,int> biggestPrimeFactor = getBiggestPrimeFactor(a);
        int factor = biggestPrimeFactor.first;
        int res = getFactorNum(n, factor);
        res /= biggestPrimeFactor.second;
        cout << res << endl;
    }
    return 0;
}
~~~

## 求root(N, k)

[求root(N, k)_牛客题霸_牛客网 (nowcoder.com)](https://www.nowcoder.com/practice/9324a1458c564c4b9c4bfc3867a2aa66?tpId=60&tqId=29488&tPage=1&ru=/kaoyan/retest/1001&qru=/ta/tsing-kaoyan/question-ranking)

**描述**

N<k时，root(N,k) = N，否则，root(N,k) = root(N',k)。N'为N的k进制表示的各位数字之和。输入x,y,k，输出root(x^y,k)的值 (这里^为乘方，不是异或)，2=<k<=16，0<x,y<2000000000，有一半的测试点里 x^y 会溢出int的范围(>=2000000000)

**输入描述**：

每组测试数据包括一行，x(0<x<2000000000), y(0<y<2000000000), k(2<=k<=16)

**输出描述**：

输入可能有多组数据，对于每一组数据，root(x^y, k)的值

思路：本题很难，需要做一定的**数论推导**，得到$N'=N\%(k-1)$的结论

同时要注意的是int类型可能无法装得下x、y，所以得用long long；同时需要用快速幂加速计算

![img](http://xherlock.top/usr/uploads/2023/06/1067085940.png)

~~~c++
#include <iostream>
using namespace std;

long long FastExponentiation(long long x, long long y, int k) {
    long long result = 1;
    while (y) {
        if (y % 2 == 1) {
            result *= x;
            result %= k;
        }
        y /= 2;
        x *= x;
        x %= k;
    }
    return result? result: k;
}

int main() {
    long long x, y;
    int k;
    while (cin >> x >> y >> k) {
        cout << FastExponentiation(x, y, k-1) << endl;
    }
}
~~~

## 计算两个矩阵的乘积

[计算两个矩阵的乘积_牛客题霸_牛客网 (nowcoder.com)](https://www.nowcoder.com/practice/ed6552d03e624ba58d16af6d57e1c3e9?tpId=40&tqId=21502&tPage=9&rp=9&ru=/ta/kaoyan&qru=/ta/kaoyan/question-ranking)

**描述**

计算两个矩阵的乘积，第一个是2*3,第二个是3*2

**输入描述**：

输入为两个矩阵，其中一个为2*3的矩阵，另一个为3*2的矩阵

**输出描述**：

一个2*2的矩阵（每一个数字后都跟一个空格）

思路：就直接写

~~~c++
#include <iostream>
using namespace std;

int main() {
    int m1[2][3], m2[3][3];
    for (int i = 0; i < 2; i++) {
        for (int j = 0; j < 3; j++) {
            cin >> m1[i][j];
        }
    }
    for (int i = 0; i < 3; i++) {
        for (int j = 0; j < 2; j++) {
            cin >> m2[i][j];
        }
    }
    for (int i = 0; i < 2; i++) {  
        for (int j = 0; j < 2; j++) {
            int n = 0;
            for (int k = 0; k < 3; k++) {
                n += m1[i][k] * m2[k][j];
            }
            cout << n << " ";
        }
        cout << endl;
    }
}
~~~

## 矩阵幂

[矩阵幂_牛客题霸_牛客网 (nowcoder.com)](https://www.nowcoder.com/practice/31e539ab08f949a8bece2a7503e9319a?tpId=67&tqId=29638&tPage=1&ru=/kaoyan/retest/1005&qru=/ta/bupt-kaoyan/question-ranking)

**描述**

给定一个n*n的矩阵，求该矩阵的k次幂，即P^k。

**输入描述**：

第一行：两个整数n（2<=n<=10）、k（1<=k<=5），两个数字之间用一个空格隔开，含义如上所示。 接下来有n行，每行n个正整数，其中，第i行第j个整数表示矩阵中第i行第j列的矩阵元素Pij且（0<=Pij<=10）。另外，数据保证最后结果不会超过10^8。

**输出描述**：

对于每组测试数据，输出其结果。格式为： n行n列个整数，每行数之间用空格隔开，注意，每行最后一个数后面不应该有多余的空格。

思路：与上一题不同，这次矩阵大小会变化，因此定义个struct Matrix和矩阵乘法函数

同时，为了减少计算时间，使用了矩阵快速幂，与普通快速幂区别在于，初始值不是1，而是单位矩阵（对角线为1，其他为0）

~~~c++
#include <iostream>
using namespace std;

struct Matrix {
    int m[10][10];
};

Matrix Multiply(Matrix a, Matrix b, int n) {
    Matrix r;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            r.m[i][j] = 0;
        }
    }
    for (int i = 0; i < n; i++) {  
        for (int j = 0; j < n; j++) {
            for (int k = 0; k < n; k++) {
                r.m[i][j] += a.m[i][k] * b.m[k][j];
            }
        }
    }
    return r;
}

Matrix FastExponentiation(Matrix x, int n, int k) {
    Matrix r;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            r.m[i][j] = 0;
        }
        r.m[i][i] = 1;
    }
    while (k) {
        if (k % 2 == 1) {
            r = Multiply(r, x, n);
        }
        k /= 2;
        x = Multiply(x, x, n);
    }
    return r;
}

int main() {
    int n, k;
    while (cin >> n >> k) {
        Matrix p;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                cin >> p.m[i][j];
            }
        }
        p = FastExponentiation(p, n, k);
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                cout << p.m[i][j];
                if (j != n -1)
                    cout << " ";
            }
            cout << endl;
        }
    }
}
~~~

## A+B for Matrices

[A+B for Matrices_牛客题霸_牛客网 (nowcoder.com)](https://www.nowcoder.com/practice/e431b3ae9efa4726b45a659b71abe124?tpId=63&tqId=29600&tPage=2&ru=/kaoyan/retest/9001&qru=/ta/zju-kaoyan/question-ranking)

**描述**

This time, you are supposed to find A+B where A and B are two matrices, and then count the number of zero rows and columns.

**输入描述**：

The input consists of several test cases, each starts with a pair of positive integers M and N (≤10) which are the number of rows and columns of the matrices, respectively. Then 2*M lines follow, each contains N integers in [-100, 100], separated by a space. The first M lines correspond to the elements of A and the second M lines to that of B.   The input is terminated by a zero M and that case must NOT be processed.

**输出描述**：

For each test case you should output in one line the total number of zero rows and columns of A+B.

思路：哎，就是一点点算；可以改进的点是读B的时候可先把行的0找出来

~~~c++
#include <iostream>
using namespace std;

int main() {
    int M, N;
    while (cin >> M >> N) {
        int A[M][N], B[M][N];
        for (int i = 0; i < M; i++) {
            for (int j = 0; j < N; j++) {
                cin >> A[i][j];
            }
        }
        for (int i = 0; i < M; i++) {
            for (int j = 0; j < N; j++) {
                cin >> B[i][j];
            }
        }
        for (int i = 0; i < M; i++) {
            for (int j = 0; j < N; j++) {
                A[i][j] += B[i][j];
            }
        }
        int cnt = 0, flag = 0;
        for (int i = 0; i < M; i++) {
            flag = 1;
            for (int j = 0; j < N; j++) {
                if (A[i][j] != 0) {
                    flag = 0;
                }
            }
            cnt += flag;
        }
        for (int i = 0; i < N; i++) {
            flag = 1;
            for (int j = 0; j < M; j++) {
                if (A[j][i] != 0) {
                    flag = 0;
                    break;
                }
            }
            cnt += flag;
        }
        cout << cnt << endl;
    }
}
~~~

## 递推数列

**描述**

给定a0,a1,以及an=p*a(n-1) + q*a(n-2)中的p,q。这里n >= 2。 求第k个数对10000的模。

**输入描述**：

输入包括5个整数：a0、a1、p、q、k。

**输出描述**：

第k个数a(k)对10000的模。

思路：乍一看，不就是递归么，刷刷写好了，测试案例也没问题，一提交，报错！超时！！！

想想也是，清华上机题能简单么

~~~c++
#include <iostream>
using namespace std;

int get_a(int a0, int a1, int p, int q, int k) {
    if (k > 3)
        return (p * get_a(a0, a1, p, q, k-1) + q * get_a(a0, a1, p, q, k-2)) % 10000;
    else if (k == 3)
        return (p * get_a(a0, a1, p, q, k-1) + q * a1) % 10000;
    else if (k == 2)
        return (p * a1 + q * a0) % 10000;
    else if (k == 1)
        return a1 % 10000;
    else
        return a0 % 10000;
}

int main() {
    int a0, a1, p, q, k;
    while (cin >> a0 >> a1 >> p >> q >> k) {
        cout << get_a(a0, a1, p, q, k) << endl;
    }
}
~~~

### 法1：while型递归

思路：这样子写递归貌似会快

~~~c++
#include <iostream>
using namespace std;

int get_a(int a0, int a1, int p, int q, int k) {
    int cnt = 2, a2;
    p %= 10000; 
    q %= 10000;
    if (k == 0)
        return a0 % 10000;
    else if (k == 1)
        return a1 % 10000;
    else {
        while (cnt <= k) {
            a2 = (p * a1 + q * a0) % 10000;
            a0 = a1;
            a1 = a2;
            cnt++;
        }
        return a1;
    }
}

int main() {
    int a0, a1, p, q, k;
    while (cin >> a0 >> a1 >> p >> q >> k) {
        cout << get_a(a0, a1, p, q, k) << endl;
    }
}
~~~

### 法2：转换为矩阵快速幂

略，不想学他了，直接复制了代码

~~~c++
#include<iostream>
#include <cstring>

using namespace std;

// 递推公式构造的矩阵大小为 2*2
const int MAXN = 2;
const int mod = 10000;

// 矩阵类，通用
struct Matrix{
    int matrix[MAXN][MAXN];
    int row, col;
    Matrix(int r, int c):row(r),col(c){
        // 构造函数内将矩阵元素全部初始化为0
        memset(matrix, 0, sizeof(matrix));
    };
};

// 计算矩阵乘法
Matrix Multiply(Matrix x, Matrix y){
    Matrix answer(x.row, y.col);
    for(int i = 0; i<answer.row; i++){
        for(int j = 0; j<answer.col; j++){
            for(int k = 0; k<x.col; k++){
                // 注意中间结果也要进行取模运算
                answer.matrix[i][j] = (answer.matrix[i][j] + x.matrix[i][k] * y.matrix[k][j]) % mod;
            }
        }
    }
    return answer;
}

// 构造单位矩阵初始化快速幂结果矩阵
Matrix InitAnswer(Matrix x){
    Matrix answer(x.row, x.col);    // 元素已全部初始化为0
    for(int i=0;i<answer.row;i++)
        answer.matrix[i][i] = 1;            // 对角线元素初始化为1，构造单位矩阵
    return answer;
}

// 核心函数：计算矩阵快速幂
Matrix FastExponentiation(Matrix x, int k){
    Matrix answer = InitAnswer(x);
    while(k>0){
        if(k%2==1)    // k为奇数则answer累乘当前x
            answer = Multiply(answer, x);
        // 矩阵平方，指数减半
        x = Multiply(x, x);
        k /= 2;   // 等价于右移一位 k>>=1;
    }
    return answer;
}

int main() {
    int a0, a1, p, q, k;
    while (cin >> a0 >> a1 >> p >> q >> k) {
        // 构造参数矩阵A
        Matrix answer(MAXN, MAXN);
        answer.matrix[0][0] = p, answer.matrix[0][1] = q;
        answer.matrix[1][0] = 1, answer.matrix[1][1] = 0;
        // 利用矩阵快速幂对参数矩阵A求解k-1次幂
        answer = FastExponentiation(answer, k - 1);
        // A的第一行乘以起始元素列向量 [a1, a0]' 即为an的值，注意大数需要随时取模
        int res = ((answer.matrix[0][0] * a1) % mod + (answer.matrix[0][1] * a0) % mod) % mod;
        cout << res << endl;
    }
    return 0;
}
~~~

最后修改：2023 年 06 月 12 日

如果觉得我的文章对你有用，请随意赞赏

发表评论取消回复

评论 *

私密评论

名称 *

🎲

邮箱 *

地址

Reverse（十一）
浏览次数: 2629
Win11新机鼓捣记录
浏览次数: 2382
栈~数制转换
浏览次数: 1604
C++学习
浏览次数: 1603
Python实现文件管理系统（重命名和删除）
浏览次数: 1575

顶点软件
你写得非常清晰明了，让我很容易理解你的观点。
mars
博主你好，请问怎么知道的alloc函数属于Buffer下的方法...
lj
该评论仅登录用户及评论双方可见
Mr.Guan
:@(赞一个)
Typecho
欢迎加入 Typecho 大家族

运输层（二）
浏览次数: 502
C语言~结构回顾
浏览次数: 522
Sqli-labs学习4
浏览次数: 827
序列密码
浏览次数: 445
数据库系统开发生命周期
浏览次数: 941

机试day8

Xherlock • 2023 年 06 月 12 日

# 机试day8

## 最大公约数

**描述**

输入两个正整数，求其最大公约数。

**输入描述**：

测试数据有多组，每组输入两个正整数。

**输出描述**：

对于每组输入,请输出其最大公约数。

思路：辗转相除法，也可以写个递归的取模函数

~~~c++
#include <iostream>
using namespace std;

## 最简真分数

**描述**

给出n个正整数，任取两个数分别作为分子和分母组成最简真分数，编程求共有几个这样的组合。

**输入描述**：

每组包含n（n<=600）和n个不同的整数，整数大于1且小于等于1000。

**输出描述**：

每行输出最简真分数组合的个数。

思路：转换为求最大公约数，如果不为1，则为最简真分数

~~~c++
#include <iostream>
using namespace std;

int is_zuijian(int a, int b) {
    int tmp;
    while (b) {
        tmp = a % b;
        a = b;
        b = tmp;
    }
    if (a != 1)
        return 0;
    else
        return 1;
}

## 素数判定

**描述**

给定一个数n，要求判断其是否为素数（0,1，负数都是非素数）。

**输入描述**：

测试数据有多组，每组输入一个数n。

**输出描述**：

对于每组输入,若是素数则输出yes，否则输入no。

思路：对于大于1的数遍历取模，若余数为0，说明存在银子，不是质数【巧妙方法：比到根号n即可，数论知识】

~~~c++
#include <iostream>
#include <math.h>
using namespace std;

int is_prime(int n) {
    int prime = 1;
    for (int i = 2; i <= sqrt(n); i++) {
        if (n % i == 0) {
            prime = 0;
            break;
        }
    }
    return prime;
}

## 素数

**描述**

输入一个整数n(2<=n<=10000)，要求输出所有从1到这个整数之间(不包括1和这个整数)个位为1的素数，如果没有则输出-1。

**输入描述**：

输入有多组数据。 每组一行，输入n。

**输出描述**：

输出所有从1到这个整数之间(不包括1和这个整数)个位为1的素数(素数之间用空格隔开，最后一个素数后面没有空格)，如果没有则输出-1。

思路：本题无非就是多了个要求**素数个位为1**，直接for循环从11每次加10，每个循环内做一次上一题的is_prime判断

~~~c++
#include <iostream>
#include <math.h>
using namespace std;

int is_prime(int n) {
    int prime = 1;
    for (int i = 2; i <= sqrt(n); i++) {
        if (n % i == 0) {
            prime = 0;
            break;
        }
    }
    return prime;
}

瞅了眼题解，发现个搞笑的：他的做法和id很搭配

![image-20230610171646980.png](http://xherlock.top/usr/uploads/2023/06/3741874374.png)

## Prime Number

**描述**

Output the k-th prime number.

**输入描述**：

k≤10000

**输出描述**：

The k-th prime number.

思路：本题依然很简单，为了应对不同可能的k值，我们可以提前先找好10000个素数存入vector，直接下标k取值就好

做了一个加速【感觉不明显】，首先已经存好2，剩下的只检查奇数

~~~c++
#include <iostream>
#include <vector>
#include <math.h>
using namespace std;

int is_prime(int n) {
    int prime = 1;
    for (int i = 2; i <= sqrt(n); i++) {
        if (n % i == 0) {
            prime = 0;
            break;
        }
    }
    return prime;
}

额外学习下：埃氏筛法

**埃氏筛法**：用已经筛选出的素数去过滤所有能整除它的数，但是只能在给定范围内快速筛选，所需时间少很多

## 质因数的个数

**描述**

求正整数N(N>1)的质因数的个数。 相同的质因数需要重复计算。如120=2*2*2*3*5，共有5个质因数。

**输入描述**：

可能有多组测试数据，每组测试数据的输入是一个正整数N，(1<N<10^9)。

**输出描述**：

对于每组数据，输出N的质因数的个数。

思路：完全没必要用书上的先求一定范围素数，在一个个遍历

可以从2开始，一个个去除N，每遇到一个余0的num++，直到N完全没有该因子

~~~c++
#include <iostream>
using namespace std;

## 约数的个数

**描述**

输入n个整数,依次输出每个数的约数的个数

**输入描述**：

输入的第一行为N，即数组的个数(N<=1000) 接下来的1行包括N个整数，其中每个数的范围为(1<=Num<=1000000000)

**输出描述**：

可能有多组输入数据，对于每组输入数据， 输出N行，其中每一行对应上面的一个数的约数的个数。

### 法1：偏暴力搜索

但是由于需要找出素因数，会耗费不少时间（假如N很大，factor++这里循环较长时间），导致程序超时【当然有解决办法，即提前算好素因数】

~~~c++
#include <iostream>
#include <vector>
#include <cmath>
using namespace std;

### 法2：因数成对出现

除了完全平方数外，都是成对出现，因此只需计算到$\sqrt{n}$即可，每次+2，如果完全平方数中间+1

~~~c++
#include <iostream>
#include <vector>
#include <cmath>
using namespace std;

## 整除问题

**描述**

给定n，a求最大的k，使n！可以被a^k整除但不能被a^(k+1)整除。

**输入描述**：

两个整数n(2<=n<=1000)，a(2<=a<=1000)

**输出描述**：

一个整数.

思路：首先本题目肯定**无法使用一般数字类型**，因为n的阶乘太大；因此需要结合因数拆解来做

这里有一些学网安数当时的味，发现很多当时学的完全可以用到现在这里

首先还是获取1000以内的素数，使用模板！！！记住它

~~~c++
const int MAXN = 1001;
vector<int> prime;
bool isPrime[MAXN];

getBiggestPrimeFactor用来获取a的最大素因数及其指数，getFactorNum获取n的阶乘中含有最大素因数个数

int getFactorNum(int n, int factor) {
    return n == 0? 0: n / factor + getFactorNum(n / factor, factor);
}

## 求root(N, k)

**描述**

**输入描述**：

每组测试数据包括一行，x(0<x<2000000000), y(0<y<2000000000), k(2<=k<=16)

**输出描述**：

输入可能有多组数据，对于每一组数据，root(x^y, k)的值

思路：本题很难，需要做一定的**数论推导**，得到$N'=N\%(k-1)$的结论

同时要注意的是int类型可能无法装得下x、y，所以得用long long；同时需要用快速幂加速计算

![img](http://xherlock.top/usr/uploads/2023/06/1067085940.png)

~~~c++
#include <iostream>
using namespace std;

int main() {
    long long x, y;
    int k;
    while (cin >> x >> y >> k) {
        cout << FastExponentiation(x, y, k-1) << endl;
    }
}
~~~

## 计算两个矩阵的乘积

**描述**

计算两个矩阵的乘积，第一个是2*3,第二个是3*2

**输入描述**：

输入为两个矩阵，其中一个为2*3的矩阵，另一个为3*2的矩阵

**输出描述**：

一个2*2的矩阵（每一个数字后都跟一个空格）

思路：就直接写

~~~c++
#include <iostream>
using namespace std;

## 矩阵幂

**描述**

给定一个n*n的矩阵，求该矩阵的k次幂，即P^k。

**输入描述**：

**输出描述**：

对于每组测试数据，输出其结果。格式为： n行n列个整数，每行数之间用空格隔开，注意，每行最后一个数后面不应该有多余的空格。

思路：与上一题不同，这次矩阵大小会变化，因此定义个struct Matrix和矩阵乘法函数

同时，为了减少计算时间，使用了矩阵快速幂，与普通快速幂区别在于，初始值不是1，而是单位矩阵（对角线为1，其他为0）

~~~c++
#include <iostream>
using namespace std;

struct Matrix {
    int m[10][10];
};

## A+B for Matrices

**描述**

This time, you are supposed to find A+B where A and B are two matrices, and then count the number of zero rows and columns.

**输入描述**：

**输出描述**：

For each test case you should output in one line the total number of zero rows and columns of A+B.

思路：哎，就是一点点算；可以改进的点是读B的时候可先把行的0找出来

~~~c++
#include <iostream>
using namespace std;

## 递推数列

**描述**

给定a0,a1,以及an=p*a(n-1) + q*a(n-2)中的p,q。这里n >= 2。 求第k个数对10000的模。

**输入描述**：

输入包括5个整数：a0、a1、p、q、k。

**输出描述**：

第k个数a(k)对10000的模。

思路：乍一看，不就是递归么，刷刷写好了，测试案例也没问题，一提交，报错！超时！！！

想想也是，清华上机题能简单么

~~~c++
#include <iostream>
using namespace std;

int main() {
    int a0, a1, p, q, k;
    while (cin >> a0 >> a1 >> p >> q >> k) {
        cout << get_a(a0, a1, p, q, k) << endl;
    }
}
~~~

### 法1：while型递归

思路：这样子写递归貌似会快

~~~c++
#include <iostream>
using namespace std;

int main() {
    int a0, a1, p, q, k;
    while (cin >> a0 >> a1 >> p >> q >> k) {
        cout << get_a(a0, a1, p, q, k) << endl;
    }
}
~~~

### 法2：转换为矩阵快速幂

略，不想学他了，直接复制了代码

~~~c++
#include<iostream>
#include <cstring>

using namespace std;

// 递推公式构造的矩阵大小为 2*2
const int MAXN = 2;
const int mod = 10000;

发表评论 取消回复

机试day8

发表评论取消回复